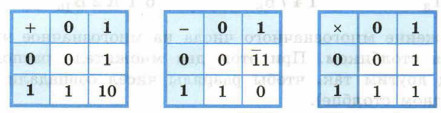
Двоичная арифметика

Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения, вычитания и умножения:

Рассмотрим несколько простых, но очень важных примеров на сложение и вычитание в двоичной системе счисления.

Пример 1.

Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения

2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ - 8⁶⁰⁰ + 6.

Представим все операнды исходного выражения в виде степеней двойки:

4²⁰¹⁶ = (2 • 2)²⁰¹⁶ = (2²)²⁰¹⁶ = 2^{2 • 2016} = 2⁴⁰³²,
8⁶⁰⁰ = (2³)⁶⁰⁰ = 2¹⁸⁰⁰,
6 = 4 + 2 = 2² + 2¹.

Исходное выражение примет вид:

2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ - 8⁶⁰⁰ + 6 = 2⁴⁰⁰⁰ + 2⁴⁰³² + 2²⁰¹⁸ - 2¹⁸⁰⁰ + 2² + 2¹.

Перепишем выражение в порядке убывания степеней:

2⁴⁰³² + 2⁴⁰⁰⁰ + 2²⁰¹⁸ - 2¹⁸⁰⁰ + 2² + 2¹.

Для работы с десятичными числами вида 2ⁿ полезно иметь в виду следующие закономерности в их двоичной записи:

2¹ = 10 = 1 + 1;
2² = 100 = 11 + 1;
2³ = 1000 = 111 + 1;
2⁴ = 10000 = 1111 + 1 и т. д.

В общем виде:

Для натуральных n и m таких, что n > m, получаем:

Эти соотношения позволят нам подсчитать количество единиц в нашем выражении, не прибегая к его вычислению.

Действительно, двоичные представления чисел 2⁴⁰³² и 2⁴⁰⁰⁰ внесут в двоичное представление суммы по одной единице. Разность 2²⁰¹⁸ - 2¹⁸⁰⁰ в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 2² и 2¹ дают ещё 2 единицы.

Итого: 1 + 1 + 218 + 1 + 1 = 222.

Пример 2. Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения

2²⁹⁹ + 2²⁹⁸ + 2²⁹⁷ + 2²⁹⁶.

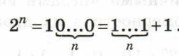
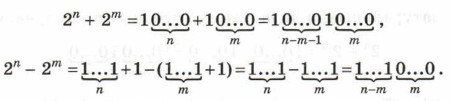
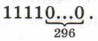Двоичное представление исходного числа имеет вид: Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой. Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.