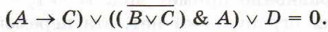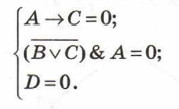Логические выражения

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.

Для логического выражения справедливо:

1) всякая логическая переменная, а также логические константы (0, 1) есть логическое выражение;

2) если А — логическое выражение, то и А — логическое выражение;

3) если А и В — выражения, то, связанные любой бинарной операцией, они также представляют собой логическое выражение.

При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:

1) отрицание;

2) конъюнкция;

3) дизъюнкция, строгая дизъюнкция;

4) импликация, эквиваленция.

Операции одного приоритета выполняются в порядке их следования, слева направо. Как и в арифметике, скобки меняют порядок выполнения операций.

Пример 1. Выясним, какие из приведённых слов удовлетворяют логическому условию (первая буква согласная → вторая буква согласная) & (последняя буква гласная → предпоследняя буква гласная):

1) ОЗОН;

2) ИГРА;

3) МАФИЯ;

4) ТРЕНАЖ.

Вычислим значение логического выражения для каждого из данных слов:

1) (0 → 1) & (0 → 1) = 1 & 1 = 1;

2) (0 → 1) & (1 → 0) = 1 & 0 = 0;

3) (1 → 0) & (1 → 1) - 0 & 1 = 0;

4) (1 → 1) & (0 → 1) = 1 & 1 = 1.

Итак, заданному условию удовлетворяют первое и четвёртое слова.

Решение логического уравнения — это один или несколько наборов значений логических переменных, при которых логическое уравнение становится истинным выражением.

Пример 2. Решим логическое уравнение

Дизъюнкция ложна в том и только в том случае, когда ложно каждое из образующих её высказываний. Иными словами, наше уравнение соответствует системе уравнений:

Окончание >>>