|
|
|
|
|
§ 18. Алгебра логики 18.3. Логические выраженияТаким образом, значение переменной D уже найдено. Импликация равна нулю в единственном случае — когда из истины следует ложь. Иначе говоря, в нашем случае: А = 1 и С = 0. Подставим найденные значения переменных в уравнение Ответ: А = 1, В = 1, С = 0, D = 0. Логические уравнения могут иметь не одно, а несколько и даже очень много решений. Зачастую требуется, не выписывая все решения уравнения, указать их количество.
Дизъюнкция истинна, если истинно хотя бы одно из образующих её высказываний. Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:
Первое равенство будет выполняться только при А = 1, В = 1 и С = 0. Поскольку D в этом уравнении не задействовано, оно может принимать любое из двух значений (0 или 1). Таким образом, всего первое уравнение имеет два решения.
Сколько решений имеет исходное уравнение?
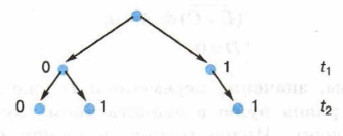
Введём замену переменных. Пусть t1 = х1 & х2, t2 = х3 & х4. Тогда исходное уравнение примет вид: t1 ↔ t2 = 1. На t1 никаких ограничений нет, эта переменная может принимать значения 0 и 1. Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t1 и t2y при которых t1 ↔ t2 = 1.
Получаем для t1 и t2 три набора значений: 00, 01, 11. Первая двоичная цифра в каждом из этих трёх наборов — результат выражения х1 & х2, вторая — х3 & х4. Рассмотрим первый набор: существует три набора х1 и х2 таких, что х1 & х2 = 0, другими словами, первый 0 мы можем получить тремя способами. Второй 0 в этом наборе мы также можем получить тремя способами. Из курсов информатики и математики основной школы вам известно одно из основных правил комбинаторики — правило умножения. Согласно ему, если элемент А можно выбрать n способами, и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами. Согласно правилу умножения, пару 00 можно получить 3 • 3 = 9 способами. Что касается пары 01, то первый 0 мы можем получить тремя способами, а для получения 1 существует единственный вариант (x3 & х4 = 1 при x3 = 1 и x4 = 1). Следовательно, есть ещё три набора переменных х1, х2, х3, х4, являющихся решением исходного уравнения.
|
|
|



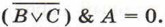 Получим:
Получим: 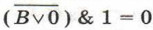 или
или  т. е. В = 1.
т. е. В = 1.
 Пример 3. Выясним, сколько различных решений имеет логическое уравнение
Пример 3. Выясним, сколько различных решений имеет логическое уравнение 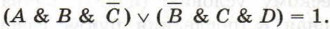
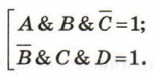
 Самостоятельно выясните, сколько решений имеет второе уравнение (из совокупности двух уравнений).
Самостоятельно выясните, сколько решений имеет второе уравнение (из совокупности двух уравнений).