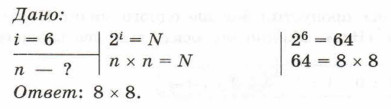|
|
|
|
|
§ 2. Подходы к измерению информации 2.1. Содержательный подход к измерению информации
Здесь первая цифра в каждой паре соответствует количеству мячей, забитых командой «Спартак», вторая — командой «Динамо». Будем считать все варианты равновероятными и отгадывать счёт, задавая вопросы, на которые можно ответить только «да» или «нет». Вопросы будем формулировать так, чтобы количество возможных вариантов счёта каждый раз уменьшалось вдвое. Это позволит нам: 1) обойтись минимальным количеством вопросов;
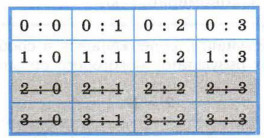
Вопрос 1. «Спартак» забил больше одного мяча? Предположим, получен ответ «Нет». Такой ответ позволяет не рассматривать варианты, расположенные в нижней части таблицы, т. е. сокращает количество возможных исходов в 2 раза:
Вопрос 2. «Спартак» забил один мяч? Предположим, получен ответ «Да». Такой ответ позволяет не рассматривать варианты, расположенные в верхней строке таблицы, т. е. сокращает количество возможных исходов ещё в 2 раза:
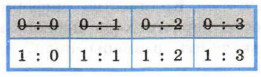
Вопрос 3. «Спартак» пропустил больше одного мяча? Предположим, получен ответ «Нет». Можно отбросить ещё два варианта:
Вопрос 4. «Спартак» пропустил один мяч? Предположим, получен ответ «Да». Получаем единственный вариант:
Итак, нам удалось выяснить счёт матча, задав четыре вопроса, ответ на каждый из которых уменьшал неопределённость результата в два раза, т. е. нёс 1 бит информации. Сообщение о счёте матча несёт четыре бита информации. 1) Да — Да — Да — Да;
Попробуйте придумать такие вопросы, чтобы цепочка ответов Нет — Да — Нет — Да приводила к счёту 2 : 3. Вычислять количество информации, содержащееся в сообщении о том, что имел место один из множества равновероятных результатов некоторого события, с помощью метода половинного деления возможно, но затруднительно. Гораздо проще воспользоваться следующей закономерностью.
При N, равном целой степени двойки (2, 4, 8, 16, 32 и т. д.), это уравнение легко решается в уме. Решать такие уравнения при других N вы научитесь чуть позже, в курсе математики 11 класса.
|
|
|



 Пример 3. О результатах футбольного матча между клубами «Спартак» и «Динамо» известно, что больше трёх мячей никто не забил. Всего возможных вариантов счёта матча — 16:
Пример 3. О результатах футбольного матча между клубами «Спартак» и «Динамо» известно, что больше трёх мячей никто не забил. Всего возможных вариантов счёта матча — 16:
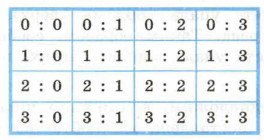


 Выясните, какому счёту матча будут соответствовать следующие цепочки ответов на поставленные выше вопросы:
Выясните, какому счёту матча будут соответствовать следующие цепочки ответов на поставленные выше вопросы:
 Количество информации i, содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из формулы:
Количество информации i, содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из формулы: