Логические функции

Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.

Совокупность значений n аргументов удобно интерпретировать как строку нулей и единиц длины п. Существует ровно 2n различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно 2^2ⁿ.

Для n = 2 существует 16 различных логических функций.

Рассмотрим их подробнее.

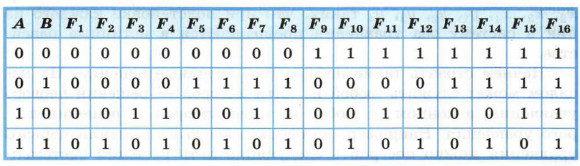
С увеличением числа аргументов количество логических функций резко возрастает. Так, для трёх переменных существует 256 различных логических функций! Но изучать их все нет никакой необходимости. Дело в том, что путём преобразований функция любого количества переменных может быть выражена через функции только двух переменных. Более того, можно использовать не все, а лишь некоторые логические функции двух переменных. Например:

1) F₂ и F₁₁ (конъюнкция и отрицание второго аргумента);

2) F₈ и F₁₃ (дизъюнкция и отрицание первого аргумента);

3) F₉ (стрелка Пирса, отрицание дизъюнкции);

4) F₁₅ (штрих Шеффера, отрицание конъюнкции).

Два последних примера говорят о том, что при желании всю алгебру логики можно свести к одной функции! Но чаще всего логические функции записываются в виде логического выражения через отрицание, конъюнкцию и дизъюнкцию.