Составление логического выражения по таблице истинности и его упрощение

Ранее мы выяснили, что для любого логического выражения можно составить таблицу истинности. Справедливо и обратное: для всякой таблицы истинности можно составить соответствующее ей логическое выражение.

Алгоритм составления логического выражения по таблице истинности достаточно прост. Для этого надо:

1) отметить в таблице истинности наборы переменных, при которых значение логического выражения равно единице;

2) для каждого отмеченного набора записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — её отрицание;

3) все полученные конъюнкции связать операциями дизъюнкции.

Пример 6. Имеется следующая таблица истинности:

После выполнения двух первых шагов алгоритма получим:

После выполнения третьего шага получаем логическое выражение:

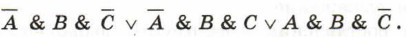
Попробуем упростить полученное логическое выражение. Прежде всего, вынесем за скобки В — общий сомножитель, имеющийся у всех трёх слагаемых, затем — сомножитель а далее используем законы алгебры логики.