|
|
|
|
|
§ 21. Элементы схемотехники. Логические схемы СумматорИз отдельных логических элементов можно составить устройства, производящие арифметические операции над двоичными числами.
Вспомним схему сложения двух п-разрядных двоичных чисел (рис. 4.9).
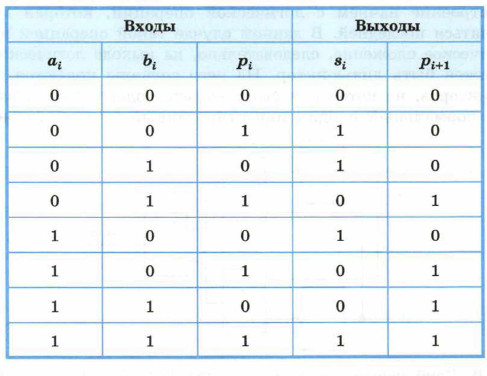
Заметим, что при сложении цифр в i-м разряде мы должны сложить цифру ai числа а, цифру bi числа b, а также pi — перенос из (i - 1)-го разряда. В результате сложения должны получиться цифра результата si и цифра переноса (0 или 1) в следующий разряд pi+1. Основываясь на этих рассуждениях, построим таблицу истинности для функций, которые в зависимости от цифр ai, bi и pi получают цифры si, и pi+1.
Вам известен алгоритм построения логического выражения по таблице истинности. Воспользуемся им и запишем выражение для функции pi+1:
Попытаемся упростить это выражение, воспользовавшись тем, что
Полученное выражение означает, что функция pi+1 принимает значение 1 только для таких комбинаций входных переменных, когда хотя бы две переменные имеют единичные значения. Обратите внимание на то, что такой вывод можно сделать и в результате анализа таблицы истинности. По таблице истинности можем записать выражение для si:
Его также можно попытаться преобразовать к более короткому виду. Но можно пойти другим путём и провести более тщательный анализ таблицы истинности для функции si. Из таблицы видно, что значение si равно 1, если все входные сигналы равны 1. Этому соответствует выражение ai & bi & pi = 1. Или значение si равно 1, если в комбинации входных сигналов есть единственная 1, т. е. единица среди переменных есть, но нет одновременно двух переменных, значения которых равны 1. Это можно записать так:
Следовательно, si можно записать так:
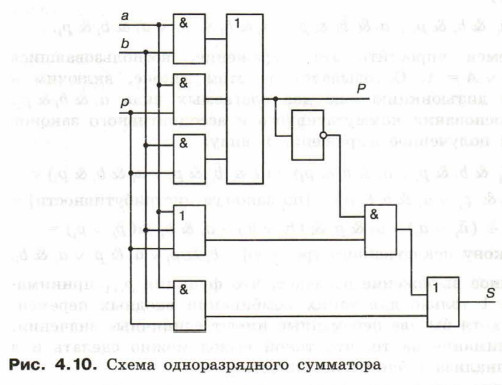
Полученные выражения позволяют реализовать одноразрядный двоичный сумматор схемой, представленной на рисунке 4.10.
Выразить si и pi+1 можно и другими формулами. Например, самое короткое выражение для st имеет вид: s = a ⊕ b ⊕ p, что позволяет построить сумматор, используя другие логические элементы.
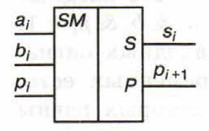
Сложение n-разрядных двоичных чисел осуществляется с помощью комбинации одноразрядных сумматоров (условное обозначение одноразрядных сумматоров приведено на рисунке слева).
|
|
|



 Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.
Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.
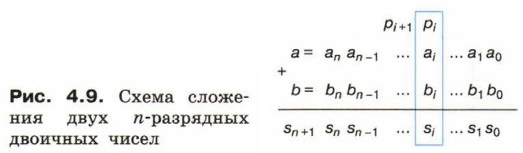
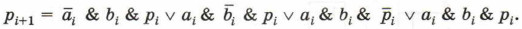
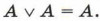 Основываясь на этом законе, включим в имеющуюся дизъюнкцию ещё два слагаемых вида аi & bi & pi, причём на основании коммутативного и ассоциативного законов преобразуем полученное выражение к виду:
Основываясь на этом законе, включим в имеющуюся дизъюнкцию ещё два слагаемых вида аi & bi & pi, причём на основании коммутативного и ассоциативного законов преобразуем полученное выражение к виду:
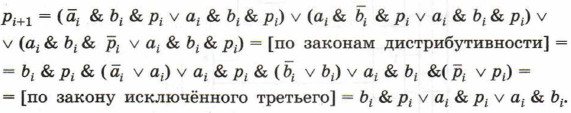
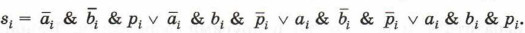
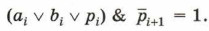
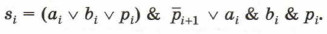
 Можно попытаться самостоятельно провести преобразование логического выражения, полученного по таблице истинности для si к итоговому виду. Но, чтобы убедиться в равносильности этих двух выражений, достаточно построить таблицу истинности для второго из них.
Можно попытаться самостоятельно провести преобразование логического выражения, полученного по таблице истинности для si к итоговому виду. Но, чтобы убедиться в равносильности этих двух выражений, достаточно построить таблицу истинности для второго из них.