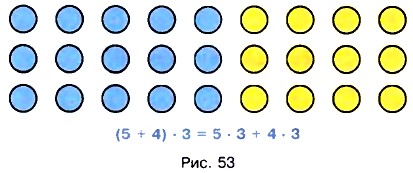
14. Упрощение выражений

Выражения (5 + 4) • З и 5 • 3 + 4 • 3 имеют одно и то же значение: (5 + 4) • 3 = 9 • 3 = 27 и 5 • 3 + 4 • 3 = 15 + 12 = 27.

На рисунке 53 видно, почему эти выражения равны.

Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения.

Это правило выражает распределительное свойство умножения относительно сложения.

С помощью букв его записывают так:

(а + b)с = ас + bс.

Одинаковые значения имеют и выражения (9 - 5) • 3 и 9 • 3 - 5 • 3, так как (9 - 5) • 3 = 4 • 3 = 12 и 9 • 3 - 5 • 3 = 27 - 15 = 12.

Для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.

Это правило называют распределительным свойством умножения относительно вычитания.

С помощью букв его записывают так:

(а - b)c = ас - bс.

Распределительное свойство умножения позволяет упрощать выражения вида 3а + 7а или 26x - 12x.
Имеем: За + 7а = (3 + 7)а = 10а.
Обычно пишут сразу: За + 7а = 10а (три а да семь а равно десяти а).
26x - 12x = (26 - 12)x = 14x.
Обычно пишут сразу: 26x - 12x = 14x (26 икс минус 12 икс равно 14 икс).

Р е ш и м уравнение Зу + 7у + 25 = 85.

Так как Зу + 7у = 10y, то уравнение можно записать так: 10y + 25 = 85.

Поэтому 10y = 85 - 25, то есть 10у = 60 и у = 60 : 10. Итак, у = 6.

П р о в е р к а: 3 • 6 + 7 • 6 + 25 = 85 — верно.

Для упрощения выражений применяют и сочетательное свойство умножения.

Например, выражение 2у • 7 • 10 заменяют на (2 • 7 • 10)y, то есть на 140у.
Пишут:
2y • 7 • 10 = (2 • 7 • 10)y = 140у.

557. Масса чашки 140 г, а масса блюдца 180 г. Купили 12 чашек с блюдцами. Сколько весит эта покупка? На сколько купленные чашки легче купленных блюдец?

558. За 1 ч работы двигатель расходует 8 л дизельного топлива. До полудня двигатель работал 5 ч, а после полудня 3 ч. Сколько литров дизельного топлива израсходовали за всё это время? На сколько больше израсходовали топлива в первой половине дня, чем во второй?

559. Найдите значение произведения с помощью распределительного свойства умножения:

а) 91 • 8;
б) 7 • 59;
в) 6 • 52;

г) 198 • 4;
д) 202 • 3;
е) 397 • 5;

ж) 24 • 11;
з) 35 • 12;
и)4 • 505;
к) 25 • 399.

560. Найдите значение выражения:

а) 69 • 27 + 31 • 27;
б) 202 • 87 - 102 • 87;
в) 977 • 49 + 49 • 23;

г) 263 • 24 - 163 • 24;
д) 438 • 90 - 238 • 90;
е) 603 • 7 + 603 • 93.

561. Примените распределительное свойство умножения:

а) (68 + а) • 2;
б) (b - 7) • 5;

в) 17(14 - х);
г) 13(2 + у).

562. При каких значениях х верно равенство:

а) 3(х + 5) = Зх + 15;
б) (3 + 5)х = Зх + 5х;
в) (7 + х) • 5 = 7 • 5 + 8 • 5;

г) (х + 2) • 4 = 2 • 4 + 2 • 4;
д) (5 - 3)х = 5х - Зх;
е) (5 - 3)х = 5х - 3 • 2?

563. Представьте в виде произведения выражение:

а) 23а + 37а;
б) 4у + 26у,
в) 48x + х;

г) у + 56у;
д) 27р - 17р;
е) 84b - 80b;

ж) 32 - ;
з) 1000 - .

564. Пусть цена 1 кг муки а р., а цена 1 кг сахара 6 р. Что означает выражение:

а) 9а + 9b; б) 9(а + b); в) 10b - 10а?

565. Расстояние между двумя сёлами 18 км. Из них выехали в противоположные стороны два велосипедиста. Один проезжает в час m км, а другой — n км. Какое расстояние будет между ними через 4 ч?

566. Найдите значение выражения:

а) 38а + 62а при а = 238; 489; б) 375b - 1756 при b = 48; 517.

567. Найдите значение выражения:

а) 32x + 32у, если х = 4, у = 26; б) 11m - 11n, если m = 308, n = 208.

568. Решите уравнение:

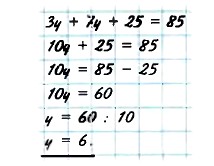
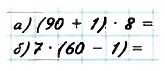
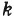а) 4x + 4х = 424;
б) 15у - 8у = 714;

в) 9z + z = 500;
г) 10 - = 702;

д) 4 + 5 + = 1200;
е) 6t + 3t - t = 6400.

Продолжение >>>