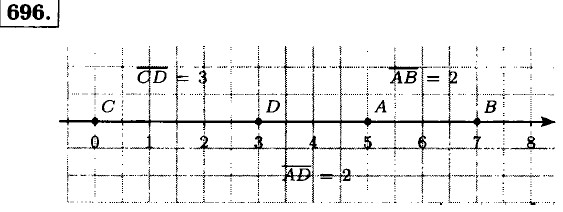
Формулы. Домашние работы (окончание)

693. a) 3² + 4² = 9 + 16 = 25;
б) (42 + 1)² = (16 + 1)² = 17² = 289;
в) (9² - 4²) : (9 - 4) = (81 - 16) : 5 = 65 : 5 = 13;
г) (8³ + 7³) : (8² - 7²) = (512 + 343) : (64 - 49) = 855 : 15 = 57.

694. Задача решена в учебнике.

695. Через 5 дней общее число прочитанных страниц книги, которую читает Сережа, будет 24 + 5 • 12 = 84, а Толя за это время прочитает 518 = 90 страниц книги. Так как 90 > 84, то Толя перегонит Сережу.

698. а) 600 < 23 • 35 < 1200 ⇒ 30 • 30 < 23 • 35 < 30 • 40; б) 2400 < 47 • 62 < 3500 ⇒ 40 • 60 < 47 • 62 < 50 • 70.

699. 1) Пусть масса одной части сплава равна х г, тогда сплав содержит 41x г меди, 8а; г олова и а: г цинка. Разность масс меди и олова равна (41x - 8x) г, а общая масса сплава равна (41x + 8x + х) г. Составим и решим уравнение: 41x - 8x = 132 ⇒ 33x = 132 ⇒ х = 132 : 33 = 4 г — масса одной части сплава, а масса куска бронзы (41 + 8 + 1) • 4 = 50 • 4 = 200 г.
2) Пусть масса одной части сплава равна х г, тогда сплав содержит 83x г алюминия, 5x г меди, х г марганца и x г магния. Разность масс меди и магния равна (5x - x) г, а общая масса сплава равна (83x + 5x + х + х) г. Составим и решим уравнение: 5x - х = 84 ⇒ 4x = 84 ⇒ х = 84 : 4 = 21 г — масса одной части сплава, а масса куска дюралюминия (83 + 5 + 1 + 1) • 21 = 90 • 21 = 1890 г.

700. Масса товара равна М = mn + р, где М — масса брутто, m — масса, одного изделия, n — число изделий, р — масса упаковки. При m = 100 г, n = 50, р = 1000 г, М = mn + р = 100 • 50 + 1000 = 6000 г = 6 кг.

701. а) При υ = 12 км/ч, t = 3 ч ⇒ s = υt = 12 • 3 = 36 км;
б) При s = 180 м, υ = 15 м/с s = υt ⇒ t = s : υ = 180 : 15 - 12 с.

702. а) При а = 15 см, b = 25 см ⇒ Р = 2 • (а + b) = 2 • (15 + 25) = 2 • 40 = 80 см.
б) При Р = 122 м, b = 34 м Р = 2 • (а + b) ⇒ а = Р : 2 - b = 122 : 2 - 34 = 61 - 34 = 27 м.

703. Периметр квадрата вычисляется по формуле Р = 4а ⇒ а = Р : 4. При Р = 144 м а = Р : 4 = 144 : 4 = 36 м.

704. Пусть масса одной части сплава равна х кг, тогда масса алюминия равна 19x кг, масса магния 2х кг. Общая масса сплава равна (19x + 2x) кг, а разность масс алюминия и магния (19x - 2х) кг. Составим и решим уравнение: 19x - 2x = 34 ⇒ 17x = 34 ⇒ x = 34 : 17 = 2 кг — масса одной части сплава, а масса сплава равна (19 + 2) • 2 = 21 • 2 = 42 кг.

705. Пусть Петя собрал х грибов, тогда Митя собрал 3x грибов. Вместе они собрали (x + 3x) грибов. Составим и решим уравнение: x + 3x = 48 + 8 ⇒ 4x = 56 ⇒ х = 56 : 4 = 14 грибов собрал Петя, а Митя собрал 143 = 42 гриба.

706. Пусть сыну х лет, тогда отцу (х + 20) лет. Составим и решим уравнение: 5х = х + 20 ⇒ 4х = 20 ⇒ х = 20 : 4 = 5 лет сыну, а отцу 5 + 20 = 25 лет.

707. а) (3х + 5х) • 18 = 144 ⇒ 8х = 144 : 18 = 8 ⇒ х = 8 : 8 = 1;
б) (7у - 3у) : 8 = 17 ⇒ 4у = 17 • 8 = 136 ⇒ у = 136 : 4 = 34;
в) (6а + а) : 13 = 14 ⇒ 7а = 14 • 13 = 182 ⇒ а = 182 : 7 = 26;
г) 48 : (9b - b) = 2 ⇒ 85 = 48 : 2 = 24 ⇒ b = 24 : 8 = 3.

708. а) 183 340 : 89 • 104 - 2060 • 104 = 214 240;
б) 102 720 : 96 • 203 = 1070 • 203 = 217 210.

<<< К началу