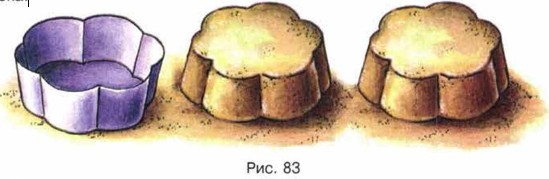
21. Объёмы. Объём прямоугольного параллелепипеда

Если наполнять формочку влажным песком, а потом переворачивать и снимать её, получатся фигуры, имеющие одинаковый объём (рис. 83). Если формочку наполнять водой, то объём воды будет равен объёму каждой фигуры из песка.

Чтобы сравнить объёмы двух сосудов, можно наполнить один из них водой и перелить её во второй сосуд. Если второй сосуд окажется заполненным, а воды в первом сосуде не останется, то объёмы сосудов равны. Если в первом сосуде вода останется, то его объём больше объёма второго сосуда. А если заполнить водой второй сосуд не удастся, то объём первого сосуда меньше объёма второго.

Для измерения объёмов применяют следующие единицы: кубический миллиметр (мм³), кубический сантиметр (см³), кубический дециметр (дм³), кубический метр (м³), кубический километр (км³).

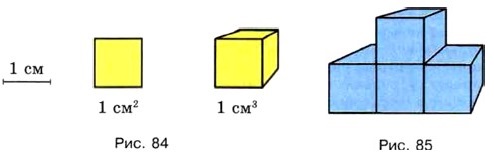
Например: кубический сантиметр — это объём куба с ребром 1 см (рис. 84).

Кубический дециметр называют также литром. 1 л = 1 дм³

Фигура на рисунке 85 состоит из 4 кубиков с ребром 1 см. Значит, её объём равен 4 см³.

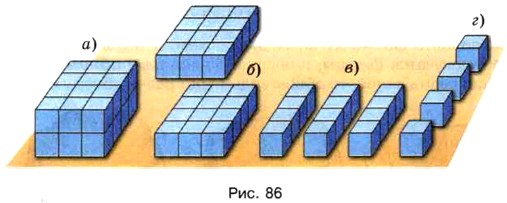
Выведем правило для вычисления объёма прямоугольного лараллелепипеда. Пусть прямоугольный параллелепипед имеет длину 4 см, ширину 3 см и высоту 2 см (рис. 86, а). Разобьём его на два слоя толщиной 1 см

(рис. 86, б). Каждый из этих слоёв состоит из 3 столбиков длиной 4 см (рис. 86, в), а каждый столбик — из 4 кубиков с ребром 1 см. (рис. 86, г). Значит, объём каждого столбика равен 4 см³, каждого слоя — 4 • 3 ( см³), а всего прямоугольного параллелепипеда — (4 • 3) • 2, то есть 24 см³.

Чтобы найти объём прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.

Формула объёма прямоугольного параллелепипеда имеет вид

V = abc.

где V — объём; а, b, с — измерения.

Если ребро куба равно 4 см, то объём куба равен 4 • 4 • 4 = 4³ (см³), то есть 64 см³.

Если ребро куба равно а, то объём V куба равен a • a • a = a³

Значит, формула объёма куба имеет вид

V = а³.

Именно поэтому запись а³ называют кубом числа а.

Объём куба с ребром 1 м равен 1 м³. А так как 1 м = 10 дм, то 1 м³ = 103 дм³, то есть 1 м³ = 1000 дм³ = 1000 л. Таким же образом находим, что

1 л = 1 дм³ = 1000 см³; 1 см³ = 1000 мм³;
1 км³ = 1 000 000 000 м³ (см. форзац).

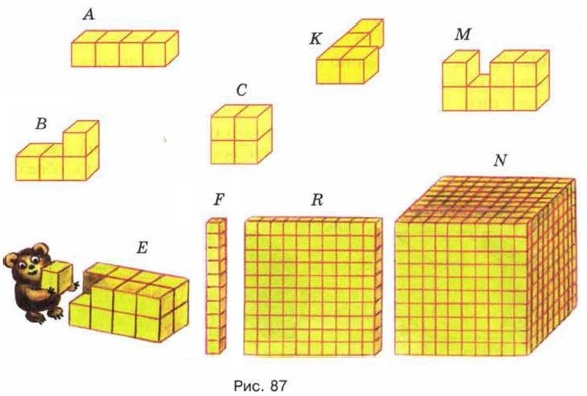
819. Из кубиков с ребром 1 см составлены фигуры (рис. 87). Найдите объёмы и площади поверхностей этих фигур.

820. Найдите объём прямоугольного параллелепипеда, если:

а) а = 6 см,    b = 10 см,    с = 5 см;
б) а = 30 дм,    b = 20 дм,    с = 30 дм;
в) а = 8 дм,    b = 6 м,    с = 12 м;
г) а = 2 дм 1 см,    b = 1 дм 7 см,    с = 8 см;
д) а = 3 м,    b = 2 дм,    с = 15 см.

Продолжение >>>