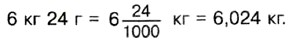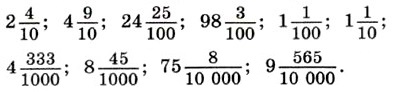|
|
|
|
|
§ 6. Десятичные дроби. Сложение и вычитание десятичных дробей 30. Десятичная запись дробных чиселВыразим расстояние 6 дм 3 см в сантиметрах: 6 дм 3 см = 63 см. Чтобы выразить то же расстояние в дециметрах, придётся использовать дроби. Так как Таким же образом находим, что
Числа со знаменателями 10, 100, 1000 и т. д. условились записывать без знаменателя.
Например, вместо Вместо Таким образом,
Любое число, знаменатель дробной части которого выражается единицей с одним или несколькими нулями, можно представить в виде десятичной записи, или, как говорят иначе, в виде десятичной дроби.
Если дробь правильная, то перед запятой пишут цифру 0.
После запятой числитель дробной части должен иметь столько же цифр, сколько нулей в знаменателе. Поэтому, например, число
1144. Запишите в виде десятичной дроби:
1145. Прочитайте десятичные дроби: а) 2,7; 11,4; 401,1; 666,6; 0,8; 9,9; 99,9; 909,9;
1146. Запишите в виде десятичных дробей числа: а) 7 целых 8 десятых; 5 целых 45 сотых; 0 целых 59 сотых; 78 целых 1 сотая; 4 целых 601 тысячная; 76 целых 32 тысячных;
1147. Запишите в виде дроби или смешанного числа: 2,7; 31,4; 567,39; 6,005; 42,78; 0,64; 0,60; 0,07; 0,99.
|
|
|



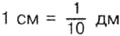 , то
, то 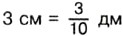 , и потому
, и потому 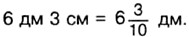
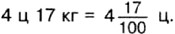 Знаменатель дробной части числа
Знаменатель дробной части числа 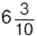 равен 10, а у числа
равен 10, а у числа 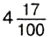 он равен 100.
он равен 100.

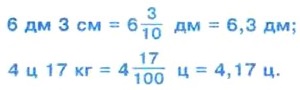

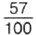 пишут 0,57 (читают: «0 целых 57 сотых»). Значит,
пишут 0,57 (читают: «0 целых 57 сотых»). Значит,
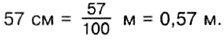

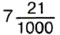 сначала надо записать так:
сначала надо записать так: 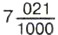 (в знаменателе 3 нуля, в числителе 2 цифры, поэтому в числителе добавляем впереди один нуль). Потом это число записываем так: 7,021 (читают: «7 целых 21 тысячная»).
(в знаменателе 3 нуля, в числителе 2 цифры, поэтому в числителе добавляем впереди один нуль). Потом это число записываем так: 7,021 (читают: «7 целых 21 тысячная»).