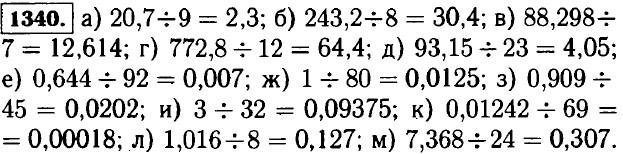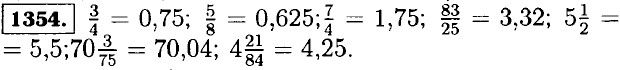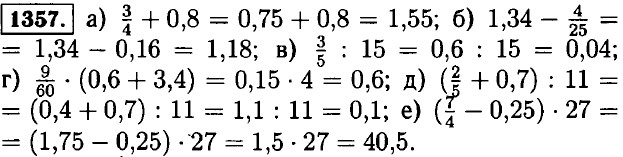Деление десятичных дробей на натуральные числа. Домашние работы

1341. Масса одних аэросаней равна (3 • 1,2 + 2) : 7 = 5,6 : 7 = 0,8 т.

1342. Ширина второго прямоугольника равна 12 • 6,6 : 11 : 8 = 79,2 : 11 = 7,2 : 8 = 0,9 см.

1343. В первый день турист прошёл 25,2 : 7 • 3 = 3,6 • 3 = 10,8 км, а во второй день 25,2 - 10,8 = 14,4 км.

1344. На консервный завод отправили 36,9 : 9 • 7 = 4,1 • 7 = 28,7 т клубники, а продали 36,9 - 28,7 = 8,2 т клубники.

1345. В первый день израсходовали 25,2 : 9 • 4 = 2,8 • 4 = 11,2 т семян, а во второй день (25,2 - 11,2) : 7 • 4 = 14 : 7 • 4 = 8т семян. После двух дней посева осталось 25,2 - (11,2 + 8) = 25,2 - 19,2 = 6 т семян.

1346. Коля пробежал дистанцию за 1,2 : 5-6 = 0,24 • 6 = 1,44 мин.

1347. Длина дороги между двумя станциями равна 16,1 : 7 • 9 = 2,3 • 9 = 20,7 км.

1348. а) 4x - х = 8,7 ⇒ 3х = 8,7 ⇒ x = 8,7 : 3 = 2,9; б) 3у + 5у = 9,6 ⇒ 8х = 9,6 ⇒ у = 9,6 : 8 = 1,2; в) а + а + 8,154 = 32 ⇒ 2а = 32 - 8,154 = 23,846 ⇒ а = 23,846 : 2 = 11,923; г) 7k - 4k - 55,2 = 63,12 ⇒ 3k = 63,12 + 55,2 = 118,32 ⇒ k = 118,32 : 3 = 39,44.

1349. Пусть в одной корзине х кг помидоров, тогда в другой корзине 2х кг. Составим и решим уравнение: х + 2х - 16,8 ⇒ 3х = 16,8 ⇒ х = 16,8 : 3 = 5,6 кг в одной корзине, а в другой 2 • 5,6 = 11,2 кг помидоров.

1350. Пусть у — площадь второго поля, тогда площадь первого поля 5у га. Составим и решим уравнение: (5у - у) = 23,2 ⇒ 4у = 23,2 ⇒ у = 23,2 : 4 = 5,8 га — площадь второго поля равна, а площадь первого поля 5 • 5,8 = 29 га.

1351. Пусть х — масса одной части, тогда 8x + 4x + 3х = 2,7 ⇒ х = 2,7 : 15 = 0,1 кг. Следовательно для приготовления 2,7 кг смеси понадобилось 8 • 0,18 = 1,44 кг яблок, 4 • 0,18 = 0,72 кг урюка и 3 • 0,18 = 0,54 кг изюма.

1352. Пусть во втором мешке х ц муки, тогда в первом мешке (x + 12) ц муки. Составим и решим уравнение: х + (х + 0,12) = 1,28 ⇒ х = (1,28 - 0,12) : 2 = 0,58 ц во втором мешке, а в первом мешке 0,58 + 0,12 = 0,7 ц муки.

1353. Пусть в первой корзине х кг яблок, тогда во второй корзине (x + 2,4) кг яблок. Составим и решим уравнение: x + ( x + 2,4) = 18,6 ⇒ x = (18,6 - 2,4) : 2 = 8,1 кг в первой корзине, а во второй корзине 8,1 + 2,4 = 10,5 кг яблок.

1355. Масса одной ноши нектара пчелы равна 100 : 16000 = 0,00625 г.

1356. Масса одной капли лекарства 30 : 1500 = 0,02 г.

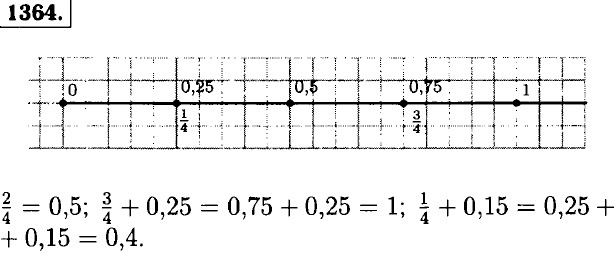
1358. а) (х - 5,46) • 2 = 9 ⇒ x = 9:2 + 5,46 = 9,96; б) (у + 0,5) : 2 = 1,57 ⇒ у = 1,57 • 2 - 0,5 = 2,64.

1359. а) 91,8 : (10,56 - 1,56) + 0,704 = 91,8 : 9 + 0,704 = 10,2 + 0,704 = 10,904; б) (61,5 - 5,16) : 30 + 5,05 = 56,34 : 30 + 5,05 = 1,878 + 5,05 = 6,928; в) 66,24 - 16,24 : (3,7 + 4,3) - 66,24 - 16,24 : 8 = 66,24 - 2,03 = 64,21; г) 28,6 + 11,4 : (6,595 + 3,405) = 28,6 + 11,4 : 10 = 28,6 + 1,14 = 29,74; д) 15,3 • 4 : 9 + 3,2 = 61,2 : 9 + 3,2 = 6,8 + 3,2 = 10; е) (4,4 + 2,4 : 8) • 3 = (4,4 + 0,3) • 3 = 4,7 • 3 = 14,1; ж) 280,8 : 12 - 0,3 • 24 = 23,4 - 7,2 = 16,2; з) (17,6 - 3 - 41,6) : 12 = (228,8 - 41,6) : 12 = 187,2 : 12 = 15,6.

1360. а) 2,5 - 1,6 = 0,9; 3,2 - 1,4 = 1,8; 0,47 - 0,27 = 0,2; 0,64 - 0,15 - 0,49; 0,71 - 0,28 = 0,43; б) 1,8 + 2,5 = 4,3; 2,7 + 1,6 = 4,3; 0,63 + 0,17 = 0,8; 0,38 + 0,29 = 0,67; 0,55 + 0,45 = 1; в) 3,4 - 0,2 = 3,2 2,6 - 0,05 = 2,55; 4,52 - 1,2 = 3,32; 4 - 0,8 = 3,2; 1 - 0,45 = 0,55; г) 5 + 0,35 = 5,35; 3,7 + 0,24 = 3,94; 0,46 + 1,8 = 2,26; 0,57 + 3 = 3,57; 1,64 + 0,36 = 2.

1361. а) 0,3 • 2 = 0,6; б) 0,8 • 3 = 2,4; в) 1,2 • 2 = 2,4; г) 2,3 • 3 = 6,9; д) 0,21 • 4 = 0,84; е) 1,6 • 5 = 8; ж) 3,7 • 10 = 37; з) 0,09 • 6 = 0,54; и) 0,18 • 5 = 0,9; к) 0,87 • 0 = 0.

1362. а) 2,9x = 2,9 ⇒ х = 1; б) 5,25x = 0 ⇒ х = 0; в) 3,7х = 37 ⇒ х = 10; г) х² = х ⇒ х = 0, 1; д) а³ = а ⇒ а = 0, 1; е) m = m³ ⇒ m = 0, 1.

1363. Выражения 2,5а увеличится на 2,5: 2,5(а + 1) - 2,5а = 2,5а + 2,5 - 2,5а = 2,5.
Значение выражения 2,5а увеличится на 5: 2,5(а + 2) = 2,5а + 5 - 2,5а = 5;
Значение выражения 2,5а увеличится в 2 раза :(2 • 2,5а) :)2,5а) = 3.

1365. а) каждое последующее число больше предыдущего на 0,6: 1,2; 1,8; 2,4; 3; 3,6; 4,2 ... ; б) каждое последующее число меньше предыдущего на 0,7: 9,6; 8,9; 8,2; 7,5; 6,8; 6,1 ... ; в) каждое последующее число больше предыдущего в 2 раза: 0,9; 1,8; 3,6; 7,2; 14,4; 28,8 ... ; г) каждое последующее число, стоящее на нечетном месте, больше предыдущего числа, стоящего на нечетном месте на 1; каждое число, стоящее на четном месте, больше предыдущего числа, стоящего на четном месте, на 0,7: 1,2; 0,7; 2,2; 1,4; 3,2; 2,1; 4,2; 2,8 ... .

<<< К началу Решенния (окончание) >>>