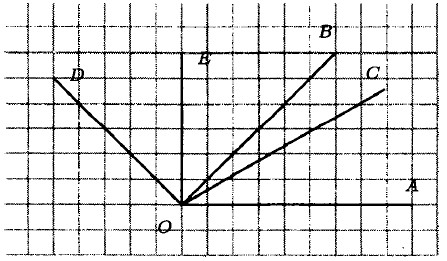
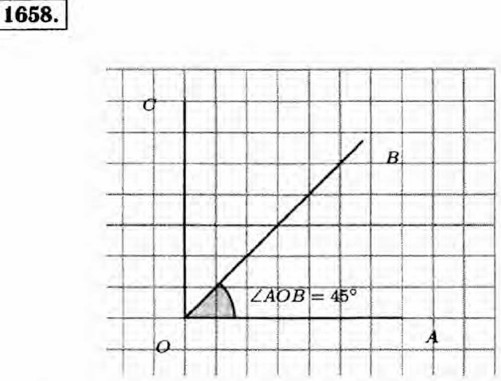
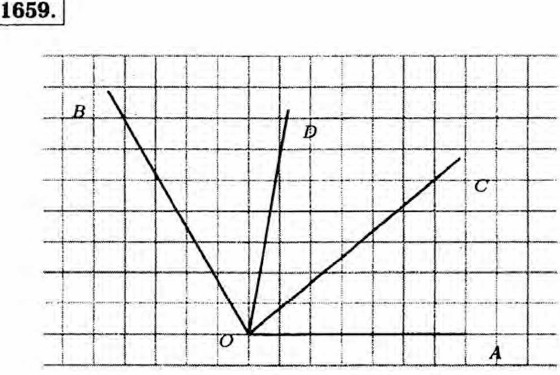
Измерение углов. Транспортир. Домашние работы

1649. a) ∠AKD = 45°, ∠AKE = 110°, ∠AKF = 155°; б) ∠BKF = 25°, ∠BKE = 70°, ∠ВКС = 120°, ∠BKD = 135°; в) ∠DKC = 60° - 45° = 15°, ∠DKE = 110° - 45° = 65°, ∠DKF = 155° - 45° = 110°, ∠CKE = 110° - 60° = 50°, ∠CKF = 155° - 60° = 95°, ∠EKF = 155° - 110° = 45°.

1650. ∠AOB = 45°, ∠AOC = 30°, ∠AOD = 135°, ∠AOE = 90°.

1651. ∠DEF = 75°, ∠PSK = 135°, ∠NOM = 112°, ∠ABC = 50°.

1652. ∠AOB = ∠AOC + ∠BOC = 37° + 19° = 56°.

1655. а) 360° : 100 • 2 = 72°; б) 60° : 100 • 25 = 15°; в) 180° : 100 • 45 = 81°; г) 90° : 100 • 80 = 72°.

1656. а) в 3 ч — угол 90°; б) в 5 ч — угол 180° : б - 5 = 150°; в) в 10 ч — угол 180° : 6 - 2 = 60°; г) в 11 ч — угол 180° : 6 = 30°; д) в 2 ч 20 мин — угол 120° - 70° = 50°; е) в 5 ч 30 мин — угол 180° - 165° = 15°.

1660. Острые углы: ∠А = 67°, ∠D = 3°. Тупые углы: ∠В = 175°, ∠С = 92°.

1661. Острые углы: ∠BAC = 20°, ∠CAD = 70°, ∠РКМ = 20°, ∠PKN = 38°, ∠MKN = 58°, ∠ХОЕ = 55°. Прямой угол: ∠BAD = 90°. Тупой угол: ∠EOV = 25°. Развернутый угол ∠XOV = 180°.

1663. а) Пусть ∠СОВ = х°, тогда ∠АОС = 3х°. Сумма ∠СОВ + ∠АОС = ∠АОВ = (х + 3х)°. Составим и решим уравнение: х + 3х = 180 ⇒ х = 180 : 4 = 45° ⇒ ∠СОВ = 45°. ∠АОС = 3 • 45 = 135°.
б) Пусть ∠СОВ = х°, тогда ∠АОС = (x + 60)°. Сумма ∠СОВ + ∠АОС = ∠АОВ = (x + x + 60)°. Составим и решим уравнение: х + х + 60 = 180 ⇒ х = (180 — 60) : 2 = 60° ⇒ ∠СОВ = 60°, ∠АОС = 60 + 60 = 120°.
в) Пусть ∠АОС = х°, тогда ∠СОВ = 4х°. Сумма ∠СОВ + ∠АОС = ∠АОВ = (х + 4x)°. Составим и решим уравнение: х + 4х = 180 ⇒ х = 180 : 5 ⇒ х = 36°⇒ ∠АОС = 36°, ∠СОВ = 4 • 36 = 144°.

1664. а) Пусть ∠СОВ = х°, тогда ∠АОС = 5х°. Сумма ∠СОВ + ∠АОС = ∠АОВ = (x + 5x) градусов. Составим и решим уравнение: х + 5х = 90 ⇒ х = 90 : 6 = 15° ⇒ ∠СОВ = 15°. ∠АОС = 5 • 15 = 75°.
б) Пусть ∠СОВ = х°, тогда ∠АОС = (90 - x)°. Сумма ∠СОВ + ∠АОС = ∠АОВ = (х - (90 - х)°. Составим и решим уравнение: х - (90 - х) = 46 ⇒ x + x - 90 = 46 ⇒ х = (46 + 90) : 2 = 68° ⇒ ∠СОВ = 68°, ∠АОС = 90 - 68 = 22°.
в) Пусть ∠АОС = х°, тогда ∠СОВ = 4х°. Сумма ∠СОВ + ∠АОС = ∠АОВ = (х + 4х)°. Составим и решим уравнение: х + 4х = 90 ⇒ х = 90 : 5 = 18° ⇒ ∠АОС = 18°, ∠СОВ = 418° = 72°.

1665. ∠АВС = ∠BCD = ∠CDA = ∠DAB = 90°; ∠АВС + ∠BCD + ∠CDA + ∠DAB = 90° + 90° + 90° + 90° = 360°; ∠АВС + ∠ВСА + ∠САВ = 180°; ∠ACD + ∠CDA + ∠DАС = 180°.

1666. ∠CAD = 110°, ∠ADC = 35°, ∠ACD = 35°; ∠CAD + ∠ADC + ∠ACD = 110° + 35° + 35° = 180°.

1667. Выполните задание самостоятельно.

<<< К началу Решенния (окончание) >>>