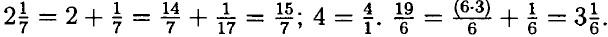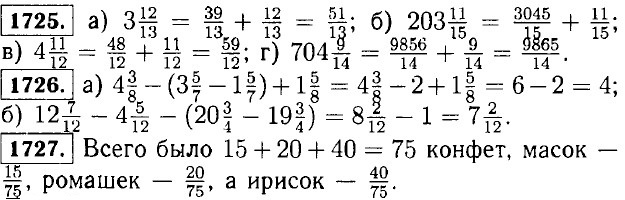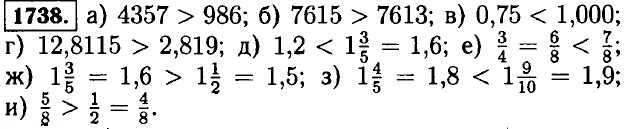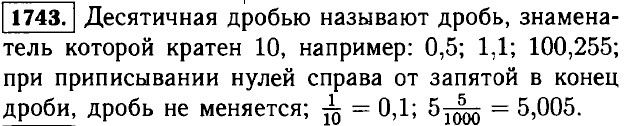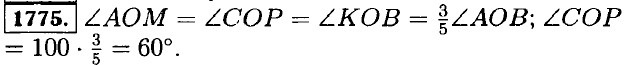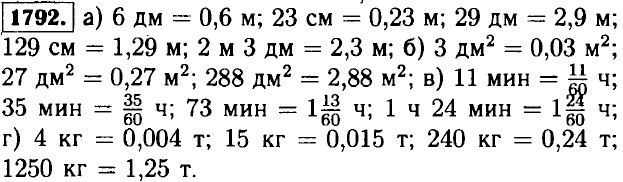|
|
|
|
Главная >> Домашние работы к учебнику Виленкина. Математика 5 класс |
|
|
Вопросы и задачи на повторение. Домашние работы1711. а) 1; 2; 100; 10000;
1712. 18; 1; 105 — натуральные числа. 1713. 6. 1714. * * *40 - * * *04 = 36. 1715. Нет, если шестизначное число оканчивается на 0. 1716. Сначала деления — слева направо, а затем сложеия — слева направо. 1717. а) 2,5, 1,2, 0,48, 0,8; б) 0,6, 0,84, 0,9, 0,5; в) 0,01, 0,38, 0,2, 1,6; г) 3,5, 0,35, 1,4, 2,44; д) 1,4, 4,2, 3,9, 6; е) 0,7, 10,5, 2,1, 7; ж) 6,6, 0,6, 7,8, 5,05; з) 6,8, 34, 3,5, 0,35. 1718. 1) 5555 + (82 320 : 84 - 693) • 66 = 5555 + (980 - 693) • 66 = 5555 + 287 • 66 - 555 + 18 942 = 24497;
1719. з) a + b = b + x; (a + b) + с = a + (b + с) б) а - (b + с) = а - b - с; а - (b -с) = а - b + с; в) а • b = b • а; (аb)с = а(bс); (а + b)с = ас + bс; (а - b)с = ас - bс. 1720. а) если второе число равно 0; б) если вычитаемое равно 0, уменьшаемое равно вычитаемому;
1721. а) 27450 = 89 • 308 + 38; б) 30394 = 307 • 99 + 1. 1722. Так как 5 < 7, то в остатке также будет 5, а неполное частное будет равно 12. 1723. а) 85 + 203x + 102x + 9 = 305x + 176; при х = 76305 • 76 + 176 = 23356; при х = 201305 • 201 + 176 = 61481; б) 79у - (23у - 15у) = 79у - 23у + 15у = 71y; при у = 1571 • 15 = 1065; при у = 30971 • 309 = 21939. 1724. Правильной называется дробь у которой числитель меньше знаменателя. Неправильной называется дробь у которой числитель больше или равен знаменателю.
1728. 4! = 1 • 2 • 3 • 4 = 24 способами.
1734. Выполните упражнение самостоятельно. 1735. а) 67(3,2), б) 67(2,8), в) 67(3) г) 67(2,99), д) C(0,85). 1736. а) А правее В; б) А и В одна и та же точка; в) A левее В. 1737. а) пятизначное всегда больше четырехзначного; б) то число, которое начинается на 7 всегда больше того, что начинается на 5; в) натуральное число всегда больше, чем 0; г) из двух обыкновенных дробей с одинаковыми знаменателями больше то, у которого больше числитель; д) из двух десятичных дробей с разными целыми частями больше то, у которой больше целая часть; е) из двух десятичных дробей с одинаковыми целыми частями больше та, у которой больше дробная часть.
1739. а) 1900 ≈ 2000; 23100 ≈ 23000; б) 0,6 ≈ 1; 0,01 ≈ 0; в) 0,052 ≈ 0,05; 10,602 ≈ 10,60. 1740. Для нахождения среднего арифметического
нескольких чисел нужно сумму этих чисел разделить на количество этих чисел.
1741.1 а) 5, 0, 0, 3,15; б) 6, 1, 0,25, 6,25; в) 4,8, 3,6, 3, 4,2; г) 3,6, 4,8, 0,12, 6; д) 9, 4,2, 6, 0,06; е) 3,8, 1,6, 2, 20; ж) 6,3, 7, 0,14, 0,8; з) 9, 1,8, 3,6, 6. 1742.1 а) 360 км; б) 180 км; в) 180 км; г) 300 км; д) 180 : 2 = 90 км/ч.
1744. а) числители складываются (вычитаются), а знаменатель остается тем же; б) как натуральные числа, с учётом запятой; в) дроби умножаются как натуральные числа, с учётом запятой; г) запятая сдвигается вправо на 1; 2; 3 знака и т. д.; д) дробь делится на число, только в частном запятая сдвигается влево на число знаков после запятой в делимом; е) число делится на дробь, только в частном запятая сдвигается вправо на число знаков после запятой в делителе; ж) в дроби запятая сдвигается влево на 1; 2; 3 знака и т. д.; з) в дроби запятая сдвигается влево на 1; 2; 3 знака и т. д.; и) в дроби запятая сдвигается вправо на 1; 2; 3 знака и т. д. 1745. а) 427051 : 839 - 390912 : 768 + 252000 : 1260 + 249249 : 249 - 509 - 509 + 200 + 1001 = 1201;
1746. а) 8 • (1,4х + 13,6y) + 13 • (0,8x - 0,6у) = 8 • 1,4х + 8 • 13,6у + 13 • 0,8х - 13 • 0,6у = 11,2х + 10,4x + 108,8у - 7,8у = 21,6x + 101у, при х = 1, у = 1 ⇒ 21,6 • 1 + 101 • 1 = 21,6 + 101 = 122,6; б) 3 • (2,9р - 1,9т) + 2 • (2,3р + 0,7m) = 3 • 2,9р - 3 • 1,9m + 2 • 2,3р + 2 • 0,7m = 8,7р - 5,7m + 4,6р + 1,4m = 13,Зр - 4,3m; при р = 0,1, m = 0 ⇒ 13,3 • 0,1 - 4,3 • 0 = 1,33. 1747. За один раз машина с двмя прицепами может перевезти 4,8 + 2,7 • 2 = 4,8 + 5,4 = 10,2 т. Тогда для перевозки 51 т зерна потребуется 51 : 10,2 = 5 поездок. 1748. Сначала завод изготавливал 560 : 14 = 40 машин в день, затем 20 - 14 = 6 дней он изготавливал по 40 + 5 = 45 машин в день. Значит за 20 дней завод изготовил 560 + 45 • 6 = 830 машин. 1749. Сейчас отец старше сына на 40 - 5 = 35 лет. Через два года отцу 40 + 2 = 42 года, сыну 5 + 2 = 7 лет. Значит отец будет старше сына в 42 : 7 = б раз. 1750. Команду можно составить 7 • 6 • 5 = 210 способами. 1751. а) из суммы вычитается известные слагаемые; б) к разности прибавляется вычитаемое; в) из уменьшаемого вычитается разность; г) произведение делится на известный множитель; д) делитель умножается на частное; е) делимое делится на частное. 1752. а) 22х + х - 10 = 59 ⇒ 23х = 59 + 10 ⇒ х = 69 : 23 = 3;
1753. В первом и втором пакетах яблок поровну, а слив во втором на 5 больше, значит, 5 слив весят 0,6 - 0,5 = 0,1 кг, тогда одна слива весит 0,1 : 5 = 0,02 кг или 20 г. 3 яблока весят 0,5 - 0,02 - 10 = = 0,3 кг. Значит, одно яблоко весит 0,3 : 3 = 0,1 кг или 100 г. 1754. Масса 1 дм3 стали равна 23,4 : 3 = 7,8 кг. Тогда 4 дм3 стали весят 7,8 • 4 = 31,2 кг. Значит, 4 дм3 стали тяжелее 4 дм3 дерева на 31,2 - 2,8 = 28,4 кг. 1755. Пусть было х мужчин, тогда женщин было Зх. Составим и решим уравнение: х + Зх - 2 - 7 + 4 + 1 = 36 ⇒ 4х = 40 ⇒ х = 10, женщин было 3 • 10 = 30. 1756. Пусть масса слоненка х, тогда масса слонихи 5х. Составим и решим уравнение: х + 5х = 7,2 ⇒ 6х = 7,2 ⇒ х = 7,2 : 6 = 1,2 т. 1757. Пусть Сене х лет, тогда: 3х - 17 = 16 ⇒ Зх = 33 ⇒ х = 11. 1758. Пусть Кате х лет, тонгда: (х + 11) : 6 = 4 ⇒ х + 11 = 4 • 6; х = 24 - 11 = 13. 1759. Пусть ночь длиться х мин, тогда день длиться х + 40 мин, а всего 24 • 60 = 1440 мин. Составим и решим уравнение: х + (х + 40) = 1440 ⇒ 2х = 1440 - 40 ⇒ х = 1400 : 2 = 700 мин = 11 ч 40 мин. 1760. Пусть прогулка у девочки длилась х минут, тогда чтение х : 3 мин. Составим и решим уравнение: х - х : 3 = 40 ⇒ 2х = 40 • 3 ⇒ х = 120 : 2 = 60 мин = 1 час. 1761. Процентом называется одна сотая часть. Чтобы найти 1% от числа, нужно число разделить на 100. Чтобы найти 5 процентов от числа, нужно число разделить на 100 и умножить на 5. 1762. Пусть в палатку отправили х т, тогда в магазин х + 1,28, а всего в палатку и магазин 3,2 : 100 • 80 = 2,56 т. Составим и решим уравнение х + (х + 1,28) = 2,56 ⇒ 2х = 2,56 — 1,28 ⇒ х = 1,28 : 2 = 0,64 т = 640 кг. 1763. На складе осталось 100 - (17 + 18 + 5) = 60% дров. Значит на складе было 6000 : 60 • 100 = 10 000 м3. В первый день продали: 10000 : 100 • 17 = 1700 м3. 1764. Пересекаются: FE и NP, FE и RQ, XY и KM, XY и LH, XY и AB, ST и KM, AB и KM, KM и NP, NP и RQ. Окружность пересекают: NP, RQ, LH, AB, KM. 1765. Выполните задание самостоятельно. 1766. а) из двух отрезков больше тот, у которого больше длина; б) из двух углов больше тот, у которого больше градусная мера. 1767. Отрезки длиной 3 см можно отложить влево 1, а вправо любое количество; длиной 7 см — влево неодного, а вправо любое количество. 1768. a) BA = DC; б) АС > СВ; в) АС = BD; г) AD > ВС. 1769. MN = MD + DC + CN = (MC - DC) + DC + DN - DC = МС + DN - DC = 6 + 5 - 2 = 9 см. 1770. PABCDE = AB + ВС + CD + DE + AE = 6,4 + 5 + 6,3 + 5,8 + 3 = 26,5 см. ABCDE — пятиугольник. 1771. а) линейки; б) транспортира.
1772. ∠BCE < 90° — острый угол, 90° < ∠DAK < 180° — тупой угол, ∠Р = 90° — прямой угол, ∠M = 180° — развернутый угол. Угол в 1° составляет щ часть развернутого угла. 1773. Лучь ОB называется биссектрисой угла МОК. 1774. Величина угла ∠D = 130°.
1776. ∠АОВ + ∠DOB = ∠AOD; ∠COD + ∠АОС = ∠AOD; ∠АОВ = ∠AOD - ∠DOB; ∠COD = ∠AOD - ∠АОС. Так как ∠DOB = ∠АОС ⇒ ∠АОВ - ∠COD. 1777. ∠АОВ = ∠COD = 180°; ∠COD = ∠АОС + ∠AOD; ∠AOB = ∠AOD + ∠BOD; ∠AOD + ∠AOC = ∠AOD + ∠BOD; ∠AOC = ∠BOD + ∠AOD - ∠AOD; ∠АОС = ∠BOD. 1778. a) 30° • 2 = 60°; 6) 5 • 30° = 150°; в) 1,5 • 30° = 45°; г) 3,5 • 3° = 10,5°; д) 4,5 • 30° = 135°. 1779. a) 2, 20, 19,2, 0,64; б) 1,4, 4,2, 0,7, 0,93; в) 7,2, 10, 3,6, 4,3; г) 75, 1,5, 0,3, 0,12; д) 5,7, 1,9, 6,3, 7; е) 0,42, 0,7, 3,5, 1; ж) 0,4, 4, 1, 0,05; з) 0,5, 0,3, 4, 0,4. 1780. Пусть х скорость Паши, тогда он догонял Борю со скоростью х - 0,2 — скорость сближения. Составим и решим уравнение: (х - 0,2) • 9 = 0,36 ⇒ х - 0,2 = 0,04 ⇒ х = 0,240 км/мин. 1781. Пусть х — скорость Коли, тогда 2х — скорость Сережи. Составим и решим уравнение: (2х - х) • 6 = 840 ⇒ х = 840 : 6 = 140 м/мин. 1782. Пусть скорость грузовой машины — х, тогда скорость легковой — 2х. Составим и решим уравнение: (х + 2х) • 4 = 480 ⇒ Зх = 480 : 4 = 120 ⇒ х = = 120 : 3 = 40 км/ч — скорость грузовой машины, а скорость легковой машины 2х = 40 • 2 = 80 км/ч. 1783. Пусть х — скорость первого поезда, тогда х + 5 — скорость второго поезда. Составим и решим уравнение: х • 3 + (х + 5) • 3 = 495 ⇒ 3х + 3х = 495 - 15 ⇒ х = 480 : 6 = 80 км/ч — скорость первого поезда, а х + 5 = 80 + 5 = 85 км/ч — скорость второго поезда. 1784. Пусть х — скорость велосипедиста, он ехал 3 + 2 = 5 часов. Составим и решим уравнение: 5x = 144 - 2 • 42 = 144 - 84 - 60 ⇒ x = 60 : 5 = 12 км/ч. 1785. Пусть х — скорость второго пешехода, тогда скорость расхождения пешеходов x + 4 км/ч. Так как они были в пути 3 ч имеем: (х + 4) • 3 = 21 ⇒ х + 4 = 7 ⇒ х = 7 - 4 = 3 км/ч. 1786. Пусть первый велосипедист ехал х часов, тогда второй ехал х - 1 ч. Составим и решим уравнение: 12x - 14(x - 1) = 64 ⇒ 12x + 14x - 14 = 64 ⇒ 26x = 64 + 14 = 78 ⇒ х = 78 : 26 = 3 ч. 1787. Катер прошёл (15,3 + 2,2) • 3 + (15,3 - 2,2) • 4 = 104,9 км. 1788. Скорость теплохода по течению 145 : 6 = 29 км/ч, а его скорость против течения 29 - 2 • 4,5 = 20 км/ч. На обратный путь он затратил 145 : 20 = 7,25 ч = 7 ч 15 мин. 1789. Выполните упражнение самостоятельно. 1790. 1 га = 100 а, 1 а = 100 м2, 1 дм2 = 100 см2, 1 м2 = 10000 см2. 1791. 1 мм2 = 0,01 см2, 1 см2 = 0,0001 м2, 1 м2 = 0,0001 га, 1 га = 0,01 км2.
<<< К началу Решенния (окончание) >>>
|
|
|



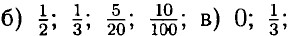 1,5; 0,001; г) 5,2; 18,5; 100,01; 0,0001.
1,5; 0,001; г) 5,2; 18,5; 100,01; 0,0001.