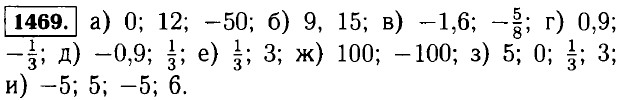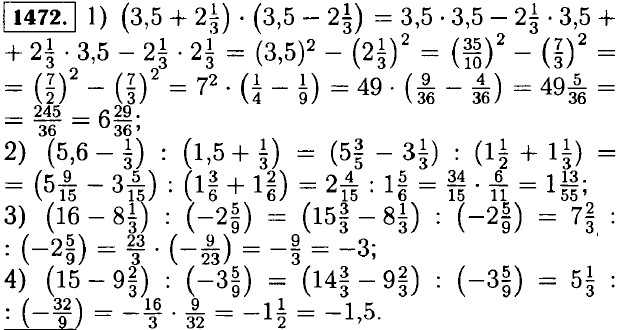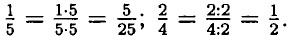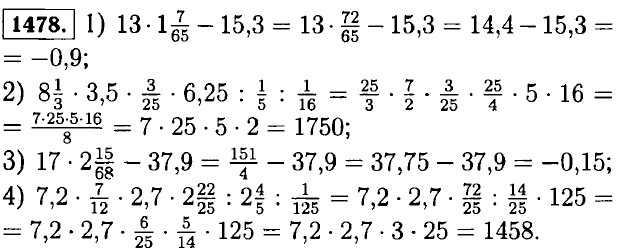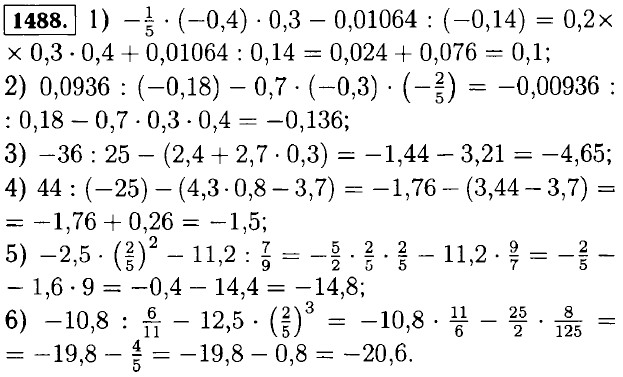Вопросы и задачи на повторение. Домашние работы

1470. а) если один из множителей равен нулю, а другой — любой; б) если делимое равно нулю, а частное нет.

1471. а) да; б) нет; в) нет; г) да.

1473. а) Делителем данного числа называют такое число, на которое делится данное. Кратным называется такое число, которое делится на данное без остатка. Например, 2 — делитель 8; 32 — кратное 16. б) Чётным числом называется целое число, которое делится на 2 без остатка. Например: 2, 4, 6. в) Число делится на 2, если оно заканчивается чётной цифрой: 0, 2, 4, 6, 8. Число делится на 3, если сумма цифр этого числа делится на 3. Число делится на 9, если сумма цифр этого числа делится на 9. Число делится на 5, если оно заканчивается цифрой 0 или 5. Число делится на 10, если оно заканчивается цифрой 10. г) Число называется простым, если оно делится только само на себя и на 1. Если число делится ещё на какое-либо число, кроме самого себя и 1, то оно называется составным. Например, 13 — простое число, 2 — простое число. Число 1 не является ни простым, ни составным.

1474. Основное свойство дроби заключается в том, что её величина не изменится, если числитель и знаменатель дроби умножить или разделить на одно и то же число. Например

1475. а) 14; 21; 28; 35; 42; б) 12; 15; 18; 21; 24; 27; 30; 33; 36; 39; в) 18; 27; 36; г) 15; 20; 25; 30; 35; 40; г) 13; 15; 17; 19; 21; 23; 25; 27; 29; 31; 33; 35; 37; 39 41.

1476. 1, 2, 3, 6, 9, 18; 1, 2, 3, 4, 6, 8, 12, 24; 1, 3, 5, 9, 15, 45.

1477. На 3 нацело делятся: 81 375; 15 8457; 67 932; 2 487 960. На 9 нацело делятся: 67932; 2487960. На 5 нацело делятся: 81 375; 2 487 960. На 15 нацело делятся: 81 375; 2 487 960.

1479. а) нет, так как например, 13 + 17 = 30; б) нет, так как например, 7 • 2 = 14; в) да, так как например: 8 • 10 = 80.

1481. а) а + b = b + а; р + (m + n) = (р + m) + n = р +m + n; б) ab = ba; a(bc) = (ab)c = abc, в) а + 0 = а; г) а • 0 = 0; а • 1 = а.

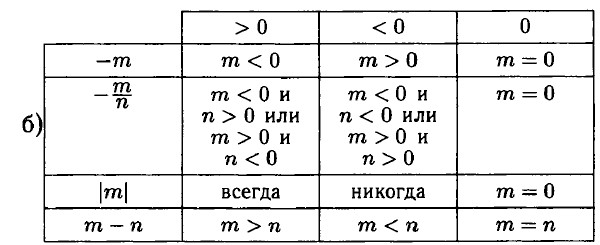
1483. а) при x > 0 ⇒ |x| = х; при х < 0 ⇒ |х| = -х; |0| = 0;

в) |-а| ≠ а; |x| ≠ -х; |-b| = |b|.

1484. Если нормальная температура тела — 36,6°С, тогда: а) с 1-го по 9-й день, то есть 9 - 1 = 8 дней; б) в 3-й день; в) с 1-го по 3-й дни температура повышалась, с 3-го по 9-й дни температура понижалась; г) с 7-го по 10-й дни; д) в 9-й и 10-й день.

I486, а) -5°С; 9,5°С; 6,5°С; б) 2 ч и в 9 ч; 10 ч 30 мин и в 23 ч; 3 ч 30 мин и 8 ч; в) температура повышалась с 5 ч 30 мин до 16 ч; понижалась с 0 ч до 5 ч 30 мин и с 16 ч до 24 ч; г) температура была положительной с 0 ч до 2 ч и с 9 ч до 24 ч; отрицательной с 2 ч до 9 ч.

1486. а) складываются числители, знаменатель не изменяется, б) дроби приводятся к общему знаменателю, после чего складываются числители, знаменатель не изменяется, в) числитель умножается на числитель, знаменатель умножается на знаменатель. г) деление состоит в умножении на обратную дробь, д) если разность двух рациональных чисел положительна, то первое число больше второго; если разность отрицательна, то второе число больше первого; если разность равна нулю, то числа равны, е) так как всякое рациональное число есть обыкновенная дробь, то их сумма — это сумма соответствующих дробей. Для чисел с разными знаками нужно взять модуль разности модулей и поставить знак большего по модулю числа, ж) вычитание положительного числа сводится к сложению с равным по модулю отрицательным числом, отрицательного — с положительным, з) умножение состоит в умножении соответствующих этим рациональным числам дробей, и) деление состоит в умножении на обратное число, к) перед членом, содержащим «+», остаётся «+», перед членом, содержащим «-», остаётся «-», если перед скобкой «+»; знаки меняются на противоположные, если перед скобкой «-».

1487. Сначала возведение в куб, потом деление, а затем вычитание.

1506. а) 8; б) -3; в) 1; г) -1; д) -15.

1507. Для приведения подобных слагаемых нужно сложить (с учётом знака) коэффициенты при общем множителе в этих слагаемых. Результатом будет произведение этой алгебраической суммы коэффициентов на общий множитель.

1508. а) 1. Перенос членов уравнения из одной части уравнения в другую с изменением перед ними знака на противоположный (12,3 и х). 2. Деление обеих частей уравнения на одно и тоже число (2). б) Деление обеих частей уравнения на одно и тоже число (-3).

1513. Пусть х — масса баллона, тогда масса плитки х - 2 кг. Общая масса туристской плитки и двух баллонов 2х + (х - 2) = 3х - 2 кг. По условию задачи, эта общая масса равна 7 кг, откуда получаем уравнение: 3х - 2 = 7 ⇒ 3х = 9 ⇒ х = 3 кг — масса баллона.

1514. Пусть х г воды вмещает кофейник. Тогда чашка вмещает х - 380 г воды. Кофейник и 2 чашки вместе вмещают: х + 2 • (х - 380) = х + 2х - 760 = 3х - 760 г воды. По условию задачи это составляет 740 г. Составим и решим уравнение: 3x - 760 = 740 ⇒ 3x = 740 + 760 ⇒ 3х = 1500 ⇒ х = 500 г — вмещает кофейник.

1515. Пусть х кг апельсинов было продано в первый день. Тогда во второй день продали х - 30 кг апельсинов, а в третий 3 • (х - 30) = 3х - 90 кг. Всего за 3 дня продано апельсинов: х + х - 30 + 3х - 90 = 5х - 120, что по условию задачи, равно 830 кг. Составим и решим уравнение: 5х - 120 = 830 ⇒ 5х = 950 ⇒ х = 190 кг апельсинов было продано в первый день.

1516. Пусть велосипедист проехал х км по лесной тропинке, тогда по просёлочной дороге он проехал 3х км, а по шоссе х + 35 км. Весь путь велосипедиста равен х + 3х + х + 35 = 5х + 35, что по условию задачи составляет 43 км. Составим и решим уравнение: 5х + 35 = 43 ⇒ 5х = 8 ⇒ х = 1,6 км проехал велосипедист по лесной тропинке. По просёлочной дороге велосипедист проехал: 3х = 3 • 1,6 = 4,8 км. По шоссе велосипедист проехал: х + 35 = 1,6 + 35 = - 36,6 км.

1518. Пусть x — площадь первого участка, тогда площадь второго участка — 60 - х га. С первого участка собрали 85x т зелёной массы, а со второго 95 • (60 - х) т. Составим и решим уравнение: 85x = 95 • (60 - х) + 1500 ⇒ 85x = 5700 - 95x + 1500 ⇒ 180x = 7200 ⇒ х = 40 га — площадь первого участка. Площадь второго участка: 60 - х = 60 - 40 = 20 га.

1519. Пусть х т силоса взяли из первой ямы, тогда из второй ямы взяли 2х т силоса. В первой яме осталось 110 - х т, а во второй 130 - 2х т. Составим и решим уравнение: 110 - х = 130 - 2х + 5 ⇒ -х + 2х = 130 + 5 - 110 ⇒ х = 25 т силоса взяли из первой ямы. Из второй ямы взяли: 2х = 50 т силоса.

1520. Пусть длина стороны ВС — х см, тогда длина стороны АВ равна х - 15 см, а длина стороны АС равна x - 15+ 22 = х + 7 см. Периметр треугольника равен 85 см. Составим и решим уравнение: x + x - 15 + x + 7 = 85 ⇒ 3x = 93 ⇒ x = 31 см — длина ВС.

1521. Составим и решим уравнение: x + (x + 1) + (x + 2) + (x + 3) = 2 ⇒ 4x + 6 = 2; x = -1, значит эти числа: -1; 0; 1; 2.

1522. Составим и решим уравнение: x + (x + 1) + (x + 2) + (x + 3) + (x + 4) = -10 ⇒ 5x + 10 = -10 ⇒ 5x = -20 ⇒ x = -4, значит эти числа: -4, -3, -2, -1, 0.

1523. Пусть х км он проплыл на теплоходе, тогда x + 120 км он проехал на поезде. Составим и решим уравнение: 8x + 4(х + 120) = 1200 ⇒ 12x + 480 = 1200 ⇒ 12x = 720 ⇒ х = 60 км.

1524. а) надо умножить данное число на дробь, б) надо разделить данное число на дробь, в) надо разделить данное расстояние на карте на реальное расстояние, или посмотреть масштаб карты, г) умножить расстояние на карте на масштаб.

1527. Из условий задачи получаем, что 52%= 0,52. В школе учится 360 : (1 - 0,52) = 360 : 0,48 = 750 человек.

1528. Из условий задачи получаем, что 12%= 0,12. Фермер снял всего 35 • 9 = 315 т овощей. Консервный завод закупил: 315 • 0,12 = 37,8 т овощей.

<<< К началу Решенния (окончание) >>>