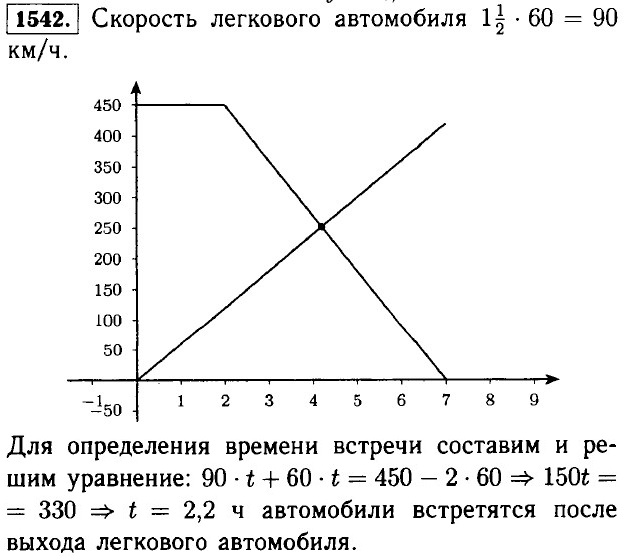
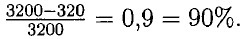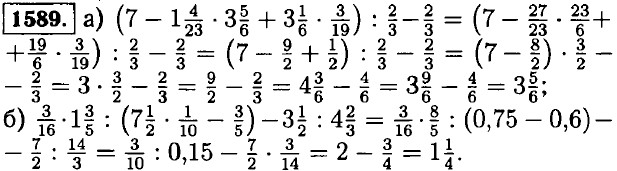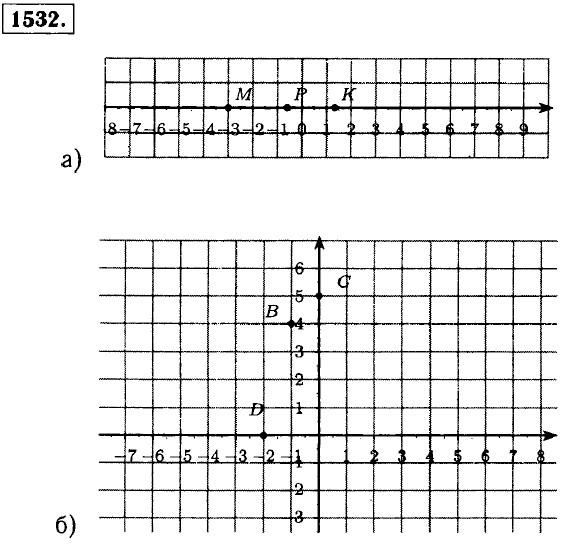
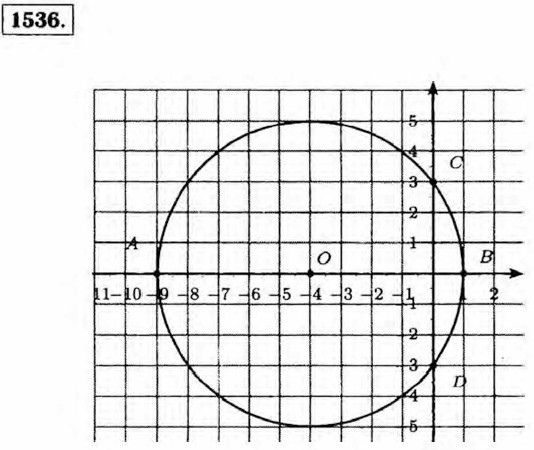
Вопросы и задачи на повторение. ГДЗ (окончание)

1531. а) на координатной прямой — одним числом; б) на координатной плоскости — двумя числами. Эти числа называют координатами.

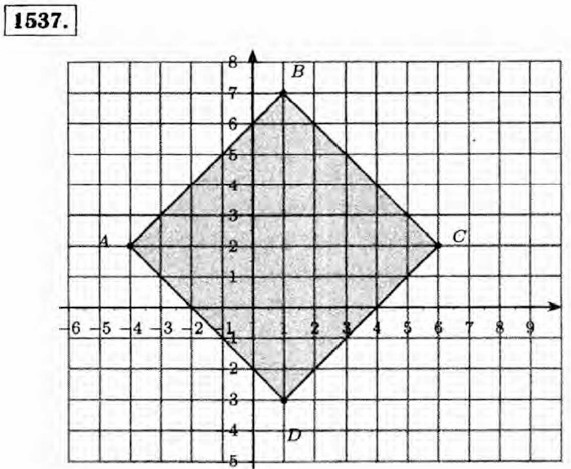
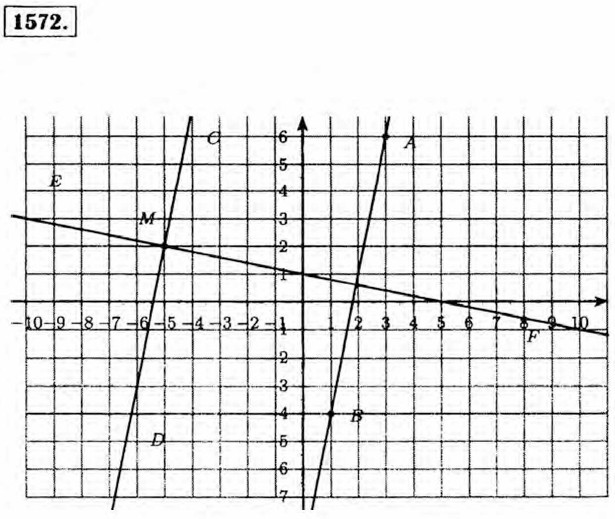
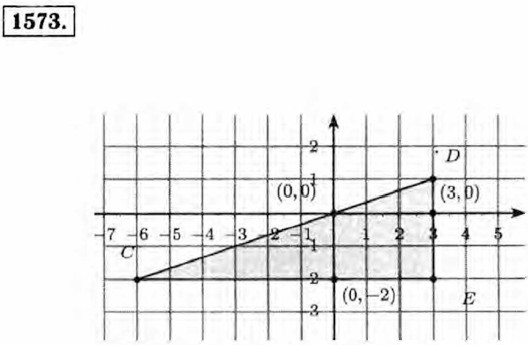
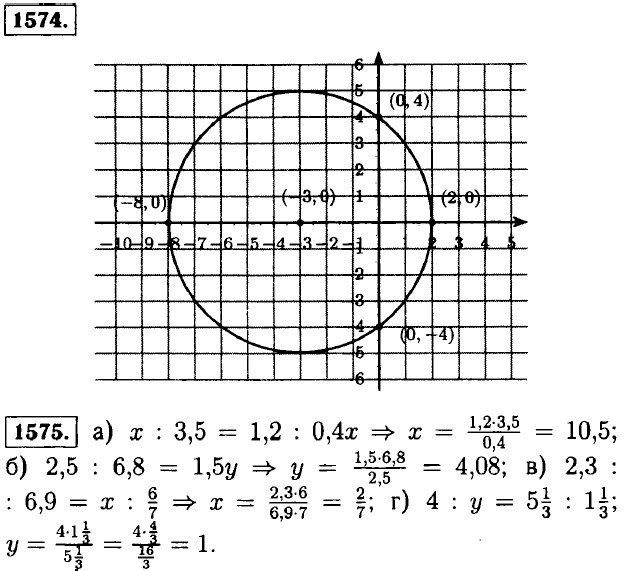
Точка В: абсцисса —1, ордината 4; Точка С: абсцисса 0, ордината 5; Точка D: абсцисса —2, ордината 0.

1533. Координаты точек пересечения: (0; 0), (-4; 0), (0; -4).

1539. Пусть х — меньшее число, тогда большее число равно 3х + 9. Составим и решим уравнение: х + 3х + 9 = 177 ⇒ 4х = 168 ⇒ х = 42 — меньшее число. Большее число: 3x + 9 = 3 • 42 + 9 = 135.

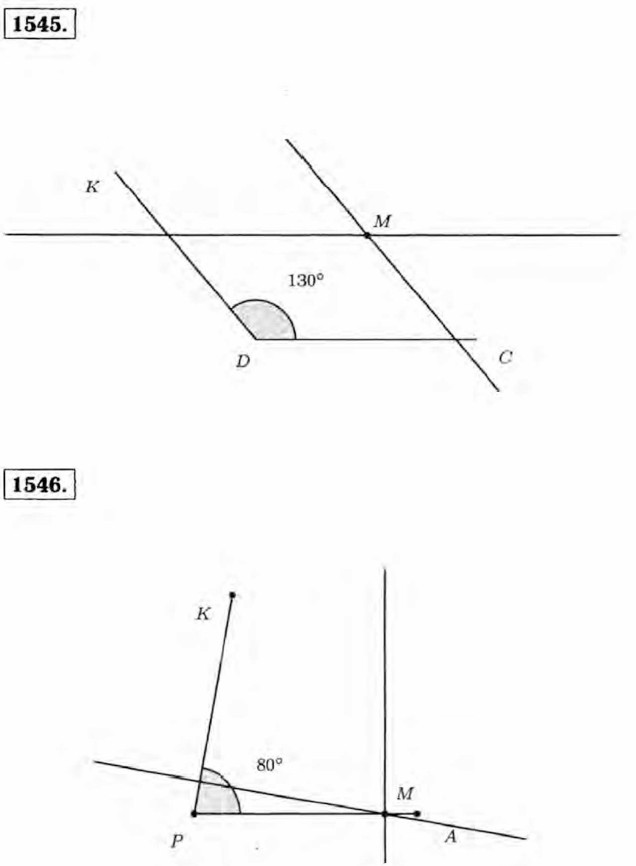
1543. Прямые называются перпендикулярными, если угол между ними 90°. Отрезки, лежащие на перпендикулярных прямых, считают перпендикулярными. Лучи перпендикулярны, если они лежат на перпендикулярных прямых.

1544. Прямые называются параллельными, если они не имеют общих точек. Отрезки, лежащие на параллельных прямых, считают параллельными.

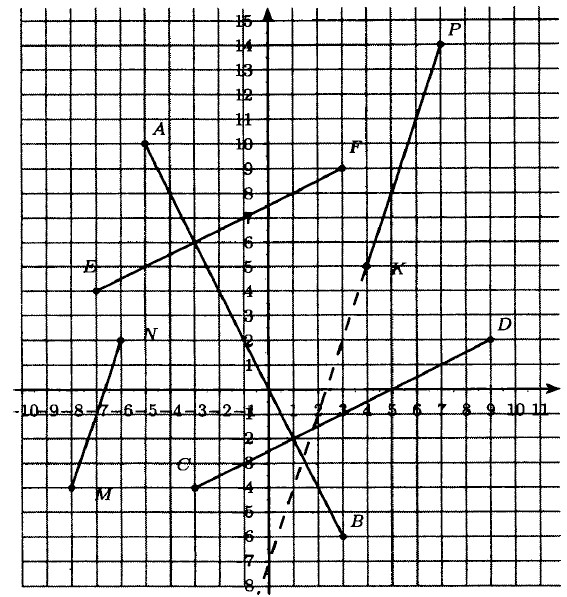
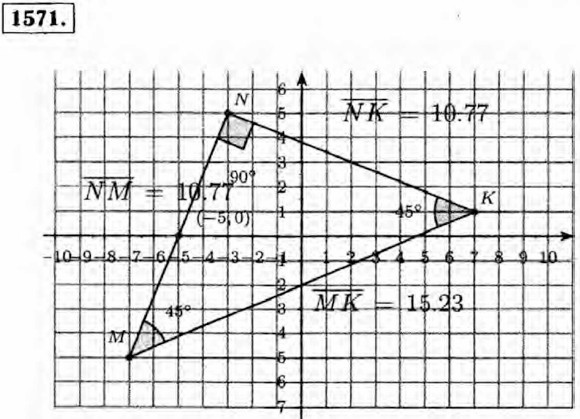
1547. CD||EF; MN|PK; AB⊥EF; AB⊥CD. Пересечения (5; 0) и (0; -7).

1548. По железной дороге отправили 100% - 69%; = 40%, что на 60% - 40% = 20% меньше, чем сплавили по реке. 20% от 32000 — это 32 000 • 0,2 = 6400 м³.

1549. По условию задачи получаем, что 20% = 0,2 и 12,5%= 0,125. Следовательно, в школу было отпущено 44 : 0,2 = 20 кг краски. Тогда на складе было 220 : 0,125 = 1760 кг краски.

1568. Пусть на втором катере было х человек, тогда на первом катере было 2х человек. Составим и решим уравнение: х -16 = 2х - 96 ⇒ х = 98 - 16 ⇒ х = 82 человека было на втором катере. На первом катере было: 2х = 164 человека.

1569. Пусть в первом элеваторе было х т зерна, тогда во втором элеваторе было 3x т зерна. Составим и решим уравнение: 3x - 960 = х + 240 ⇒ 2х = 1200 ⇒ х - 600 т зерна было в первом элеваторе. На втором элеваторе было: 3x = 3 • 600 = 1800 т зерна.

1570. Пусть в первом составе было х вагонов, в другом составе было 2а: вагонов. Составим и решим уравнение: 2х - 14 = х + 14 ⇒ х = 28 вагонов было в первом составе. Во втором составе было: 2х = 56 вагонов.

1576. Из свёклы получится: 2629 • 0,12 = 315,54 т сахара.

1577. Мужчины составляют 100% - 34,5% = 65,5% = 0,65 работающих на фабрике. Всего рабочих 262 : 0,655 = 400 человек.

1578. Экспедиция прошла по долине реки 100% - 40% - 26% = 34% = 0,34. Значит всего экспедиция прошла 102 : 0,34 = 120 км. По степи было пройдено: 300 • 0,4 = 120 км. По горной местности было пройдено: 300 • 0,26 = 78 км.

1579. Из условий задачи получаем, что 30%= 0,3 и 25% = 0,25. Всего в книге страниц: 180 : (1 - 0,3 - 0,25) = 180 : 0,45 = 400. В первый день Андрей прочитал 400 • 0,3 = 120 страниц.

1585. а) (112 : 28 - 36 - 24) : (-1,4) = -(4 - 60) : 1,4 = -(-56) : 1,4 - 56 : 1,4 - 40; б) 4,9 - 4,8 : : (3 - 19) - 1,4 : (-8) = 4,9 - 4,8 : (-16) + 1,4 : 8 = 4,9-4,8 : (-16) + 1,4 : 8 = 4,9 + 0,3 + 0,175 = 5,375; в) -5,7 : (-19) - 0,8 • (-4) + 2,7 : 0,3 = 0,3 + 3,2 + 9 = - 12,5; г) (-6,4 • 0,3 + 5,4 • 0,3) : (-0,2) - 5,1 = 0,3 : 0,2-5,1 = 1,5 - 5,1 = -3,6.

1586. По определению: 100 м² = 0,01 га; 3200 кг = 32 ц. В открытом грунте на 1 га выращивают 800 : 2,5 = 320 ц огурцов. В теплице выращивают: 32 : 0,01 = 3200. Значит в теплице урожайность больше на:

1587. Пусть в каждой бригаде было х человек. Составим и решим уравнение: 3 • (х - 2) = х + 8 ⇒ 3х - 6 = x + 8 ⇒ 2х = 14 ⇒ x = 7 человек.

1588. Пусть шаг Толи — х см, тогда шаг Пети x + 12 см. Составим и решим уравнение: 4(x + 12) + 54 = 6x ⇒ 4х + 48 + 54 = 6x ⇒ 2х = 102 ⇒ х = 51 см — шаг Толи, а шаг Пети: х +12 = 51 + 12 = 63 см.

1590. По определению: 1 ч 15 мин = 1,25 ч; 1 ч 30 мин = 1,5 ч. Пусть х — реальная скорость машины, тогда возможная её скорость х - 10 км/ч. Составим и решим уравнение: 1,25x = 1,5(x - 10) ⇒ 1,25x = 1,5x - 15 ⇒ 0,25x - 15 ⇒ х - 60 км/ч — скорость машины. Расстояние от города до совхоза: 1,25 • 60 = 75 км.

1593. Примем, что х — скорость течения. Составим и решим уравнение: 15 • (70 - x) = 13 • (70 + x) ⇒ 1050 - 15x = 910 + 13x ⇒ 28x = 140 ⇒ х = 5 км/ч.

<<< К началу