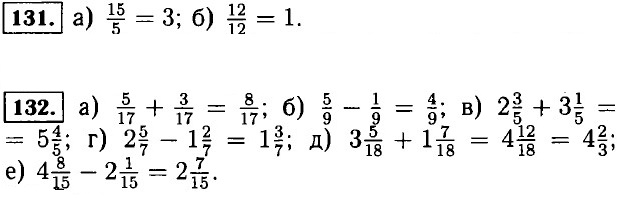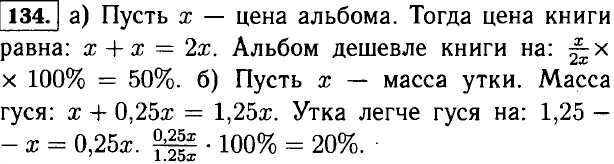Разложение на простые множители. Домашние работы

121. а) 216 = 2 • 108 = 2 • 2 • 54 = 2 • 2 • 2 • 27 = 2 • 2 • 2 • 3 • 9 = 2 • 2 • 2 • 3 • 3 • 3;
162 = 2 • 81 = 2 • 3 • 27 = 2 • 3 • 3 • 9 = 2 • 3 • 3 • 3 • 3;
144 = 2 • 72 = 2 • 2 • 36 = 2 • 2 • 2 • 18 = 2 • 2 • 2 • 2 • 9 = 2 • 2; 2 • 2 • 3 • 3;
512 = 2 • 256 = 2 • 2 • 128 = 2 • 2 • 2 • 64 = 2 • 2 • 2 • 2 • 32 = 2 • 2 • 2 • 2 • • 16 = 2 • 2 • 2 • 2 • 2 • 2 • 8 = 2 • 2 • 2 • 2 • 2 • 2 • 2 • 4 = 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2;
675 = 5 • 135 = 5 • 5 • 27 = 5 • 5 • 3 • 9 = 5 • 5 • 3 • 3 • 3; 1024 = 2 • 512 = 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2;
б) 60 = 2 • 30 = 2 • 2 • 15 = 2 • 2 • 3 • 5;
180 = 2 • 90 = 2 • 2 • 45 = 2 • 2 • 3 • 15 = 2 • 2 • 3 • 3 • 5; 220 = 2 • 110 = 2 • 2 • 55 = 2 • 2 • 5 • 11;
350 = 2 • 175 = 2 • 5 • 35 = 2 • 5 • 5 • 7;
400 = 2 • 200 = 2 • 2 • 100 = 2 • 2 • 2 • 50 = 2 • 2 • 2 • 2 • 25 = 2 • 2 • 2 • 2 • 5 • 5;
1200 = 3 • 400 = 2 • 2 • 2 • 2 • 3 • 5 • 5;
8000 = 2 • 4000 = 2 • 2 • 5 • 400 = 2 • 2 • 2 • 2 • 2 • 2 • 5 • 5 • 5;
в) 11 = 1 • 11;
1001 = 7 • 143 = 7 • 11 • 13;
1225 = 5 • 245 = 5 • 5 • 49 = 5 • 5 • 7 • 7.
21 780 = 2 • 10890 = 2 • 2 • 5445 = 2 • 2 • 5 • 1089 = 2 • 2 • 3 • 5 • 363 = 2 • 2 • 3 • 3 • 5 • 121 = 2 • 2 • 3 • 3 • 5 • 11 • 11;
45 630 = 2 • 22815 = 2 • 3 • 7605 = 2 • 3 • 3 • 2535 = 2 • 3 • 3 • 3 • 845 = 2 • 3 • 3 • 3 • 5 • 169 = 2 • 3 • 3 • 3 • 5 • 13 • 13.

122. а) 25 = 5 • 5; 49 = 7 • 7; б) 27 = 3 • 3 • 3.

123. а) 22 = 2 • 11; 33 = 3 • 11; 55 = 5 • 11; 77 = 7 • 11; б) 26 = 2 • 13; 39 = 3 • 13; 65 = 5 • 13; 91 = 7 • 13; 69 = 3 • 23; в) 46 = 2 • 23; г) 94 = 2 • 47.

124. а) а : b = (2 • 2 • 2 • 3 • 5 • 7) : (2 • 3 • 7) = 2 • 2 • 5 = 20; б) а : b = (3 • 3 • 5 • 5 • 11) : (3 • 3 • 5) = 5 • 11 = 55; в) а : b = (3 • 3 • 5 • 7 • 13) : (3 • 5 • 5 • 13) = (3 • 7) : 5 = 21 : 5, не делится; г) а : b = (2 • 3 • 3 • 7 • 7) : (3 • 7) = 2 • 3 • 7 = 42; д) а : 6 = (2 • 2 • 3 • 3 • 3 • 5 • 7) : (3 • 3 • 3 • 5) = 2 • 2 • 7 = 28; е) а : b = (2 • 2 • 2 • 3 • 3 • 5 • 5 • 5) : (2 • 2 • 2 • 5 • 5 • 5) = 3 • 3 = 9.

125. а) 6; 2,307; 4,7; 5; 12,9; б) 0,64; 0,52; 0,98; 0,15; 0,55; в) 0,016; 0,5; 0,012; 23; 400; г) 3,1; 1,7; 47; 31 49,3.

126. При а = 1, 23а = 23 • 1 = 23.

127. Не существует, так как при вычислении периметра сумма сторон умножается на два: Р = 2 • (а + b).

128. Число 54 — 2, 3; число 62 — 2, 31; число 143 — 11, 13; число 182 — 2, 7; число 3333 — 3, 11; число 5005 — 5, 7.

129. 19, 23, 29, 31, 37, 41, 43.

130. Координаты точек: А(р - 1), В(р + 1), С(2р), D(3p). Если р простое число, то оно нечётное, тогда числа р - 1 и р + 1 — чётные, поэтому р - 1 и р + 1 — составные числа, за исключением р = 3 (3 - 1 = 2, 2 — простое число). 2р и 3р — составные числа, так как содержат множители 2 и 3.

133. 35 - 3 = 32 выписывают газету или журнал; 32 - 22 = 10 выписывают только газету; 32 - 27 = 5 выписывают только журнал; 10 + 5 = 15 выписывают или газету, или журнал; 32 - 15 = 17 выписывают и газету, и журнал.

135. а) (7,46 + 8,7) : 0,016 + 6,9; б) 20 - (10,2 + 8,83).

136. а) Р = 12 + 17 + х, где Р — периметр прямоугольника; б) у треугольника сумма двух любых сторон всегда больше третьей стороны, поэтому 12 + 17 > х ⇒ х < 29 и х + 12 > 17 ⇒ х > 5. Из двух неравенств получаем условие: 5 < х < 29.

<<< К началу Решенния (окончание) >>>