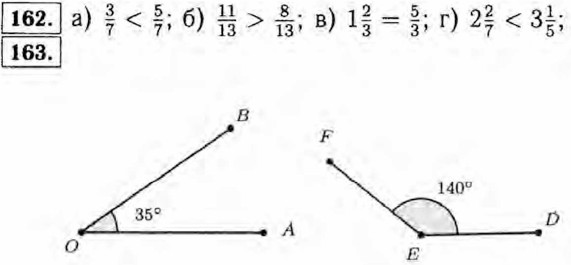
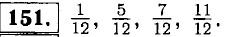|
|
|
|
√лавна€ >> ƒомашние работы к учебнику ¬иленкина. ћатематика 6 класс |
|
|
І 1. ƒелимость чисел Ќаибольший общий делитель. ¬заимно простые числа. ƒомашние работы146. а) число 18. ≈го делители: 1, 2, 3, 6, 9, 18. „исло 60. ≈го делители: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. »х общие делители: 1, 2, 3, 6;
147. ќбозначим наибольший общий делитель чисел а и b через Ќќƒ(а; b).
148. а) 12 = 2 Х 2 Х 3; 18 = 2 Х 3 Х 3; Ќќƒ(12; 18) = 2 Х 3 = 6;
149. а) Ќет, не €вл€ютс€. Ќќƒ(35;40) = 5. б) ƒа, €вл€ютс€. Ќќƒ(77; 20) = 1; в) ƒа, €вл€ютс€ взаимно простыми. Ќќƒ(10; 30; 41) = 1; г) Ќет, не €вл€ютс€. Ќќƒ(231; 280) = 7. 150. 19 = 3 Х 3 Х 1; 14 = 2 Х 7 Х 1; 15 = 3 Х 5 Х 1; 27 = 3 Х 3 Х 3 Х 1. ” пар чисел 9 и 14, 14 и 15, 14 и 27 Ќќƒ = 1, эти пары чисел взаимно простые.
152. ¬се подарки одинаковые, в каждом подарке одинаковое количество апельсинов и €блок. Ќадо найти Ќќƒ(123; 82) = Ќќƒ(3 Х 41; 2 Х 41) = 41. –еб€т на Єлке было 41. ¬ каждом подарке было: 123 : 41 = = 3 апельсина и 82 : 41 = 2 €блока. 153. ¬о всех автобусах одинаковое число мест, все места были зан€ты. Ќадо найти Ќќƒ(424, 477) = Ќќƒ(2 Х 2 Х 2 Х 53; 3 Х 3 Х 53) = 53. ¬ каждом автобусе было по 53 места. ¬ лес поехало: 424 : 53 = 8 автобусов, на озеро: 477 : 53 = 9 автобусов. ¬сего было выделено: 8 + 9 = 17 автобусов. 154. а) 7, 3,5, 3,2, 8; б) 0,5, 0,1, 2,1, 3; в) 3,2, 4, 0,4, 0,2; г) 0,96, 3,2, 3, 0.3; д) 0.3, 1,5, 0,1, 10. 155. — помощью линейки или циркул€ находим, что числа а (а = 5 Х 2 = 10), b (b = 13 Х 2 = 26), с (с = 5 Х 3 = 15) Ч составные. 156. а) Ќет. —умма всех рЄбер куба равна 12 Х а Ч это составное число, б) Ќет. ѕлощадь поверхности куба равна 6 Х а2 Ч это составное число. 157. а) 875 = 5 Х 5 Х 5 Х 7; 2376 = 2 Х 2 Х 2 Х 3 Х 3 Х 3 Х 11; 2565 = 3 Х 3 Х 5 Х 5 Х 5 Х 5;
158. „исло можно разложить на простые множители только одним способом, поэтому число, которое разлагаетс€ на 2 простых множител€, не может равн€тьс€ числу, которое разлагаетс€ на 3 простых множител€. 159. Ќет нельз€, так как произведение двух простых чисел Ч это составное число, а оно может быть представлено в виде произведени€ простых множителей только одним способом. 160. ¬сего способов размещени€ 9 пассажиров в 9 - местном микроавтобусе 9 Х 8 Х 7 Х 6 Х 5 Х 4 Х 3 Х 2 Х 1 = 360880. ≈сли одни пассажир с€дет р€дом с водителем, то 8 Х 7 Х 6 Х 5 Х 4 Х 3 Х 2 Х 1 = 40320. 161. а) 15; б) 10; в) 26; г) 115.
<<< началу –ешенни€ (окончание) >>>
|
|
|