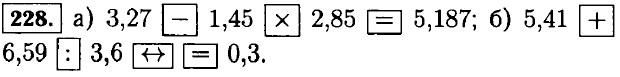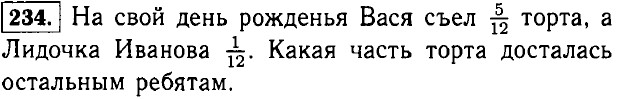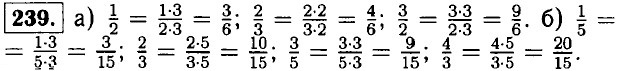Основное свойство дроби. ГДЗ

230. 1) 375 = 3 • 5 • 5 • 5; 8505 = 3 • 3 • 3 • 3 • 3 • 5 • 7; 41472 = 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 3 • 3 • 3 • 3;
2) 425 = 5 • 5 • 17; 4225 = 5 • 5 • 13 • 13; 8775 = 3 • 3 • 3 • 5 • 5 • 13.

231. 1) НОК(2450; 3500) = НОК(2 • 5 • 5 • 7 • 7; 2 • 2 • 5 • 5 • 5 • 7) = 2 • 2 • 5 • 5 • 5 • 7 • 7 = 24 500; НОД(2450; 3500) = 2 • 5 • 5 • 7 = 350.
2) НОД(792; 2178) = НОД(2 • 2 • 2 • 3 • 3 • 11; 2 • 3 • 3 • 11 • 11) = 2 • 3 • 3 • 11 = 198; НОК(729; 2178) = 2 • 3 • 3 • 11 • 11 • 2 • 2 = 8712.

232. Команду можно составить 12 • 11 • 10 • 9 способами. Распределить этапы эстафеты можно 4 • 3 • 2 • 1 = 4 = 24 способами.

233. 1) Первая часть пути была пройдена за 48,6 : 12,15 = 4 ч. После привала школьники проехали 79,2 - 48,6 = 30,6 км. Вторая часть пути была пройдена за: 30,6 : 15,3 = 2 ч. Всего поход длился: 4 + 2,5 + 2 = 8,5 ч.
2) До привала партизаны прошли: 5,2 • 4,5 = 23,4 км. По болотистой местности было пройдено: 34,2 - 23,4 = 9 км. На дорогу по болотистой местности затрачено: 9 : 2,5 — 3,6 ч. На весь переход партизаны затратили: 4,5 + 1,6 + 3,6 = 9,7 ч.

235. 8,12 • 0,25 + 3,24 • 0,25 = 2,03 + 0,81 = 2,84.

236. а) 2,835 : 0,225 • 4,537 - 32,929 = 12,6 • 4,537 - 32,929 = 57,1662 - 32,929 = 24,2372 « 24,24;
б) (4,976 + 15,2473) • 2,14 - 5,0784 = 20,2233 • 2,14 - 5,0784 = 43,277 862 - 5,0784 = 38,199 462 ≈ 38,20.

240. а) НОД(18; 36) = НОД(2 • 3 • 3; 2 • 2 • 3 • 3) = 2 • 3 • 3 = 18; НОК(18; 36) = 2 • 2 • 3 • 3 = 36; б) НОД(33; 44) = НОД(3 • 11; 2 • 2 • 11) = 11; НОК(33; 44) = 2 • 2 • 3 • 11 = 132; в) НОД(378; 441) = НОД(2 • 3 • 3 • 3 • 7; 441 = 3 • 3 • 7 • 7) = 3 • 3 • 3 • 7; НОК(378; 441) = 3 • 3 • 7 • 7 • 2 • 3 = 2646; г) НОД(11340; 37800) = НОД(2 • 2 • 3 • 3 • 3 • 3 • 5 • 7; 2 • 2 • 2 • 3 • 3 • 3 • 5 • 5 • 7) = 2 • 2 • 3 • 3 • 3 • 3 • 5 • 7= 11 340; НОК(11340; 37 800) = 37 800 • 3 = 113 400.

241. а) 2,45 • (m - 8,8) = 4,41 ⇒ m - 8,8 = 4,41 : 2,45 ⇒ m - 8,8 = 1,8 ⇒ m = 1,8 + 8,8 = 10,6; б) 7,54k - 3,6k = 5,91 ⇒ 3,94k = 5,91 ⇒ k = 1,5.

<<< К началу