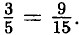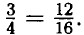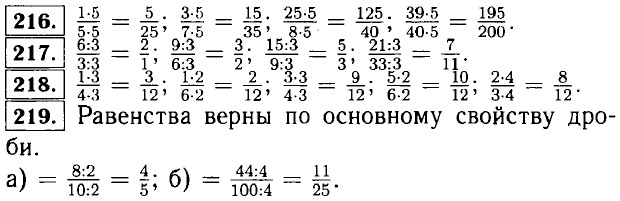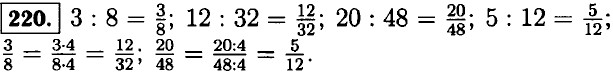|
|
|
|
Главная >> Домашние работы к учебнику Виленкина. Математика 6 класс |
|
|
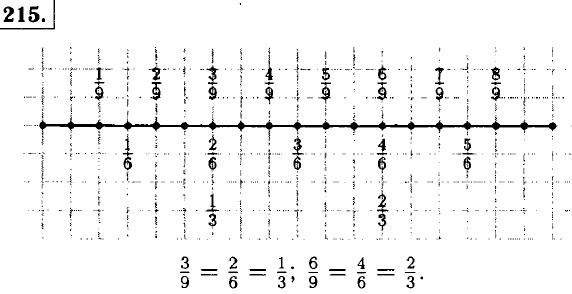
§ 2. Сложение и вычитание дробей с разными знаменателями Основное свойство дроби. Домашние работы211. Круг разделён на 15 равных частей. Закрашено 9 частей. Не закрашено 6. Если считать за одну часть три маленькие части, то будет закрашено 3 такие части а всего будет 5 таких частей, поэтому
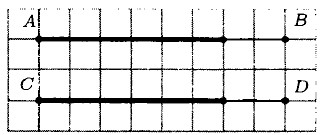
214. Выделенные части отрезков АВ и CD равны.
221. а) х = 2; б) m = 10; в) n = 3; г) у = 18. 222. а) 500, 4, 300, 140; б) 5, 200, 4, 76; в) 12,6, 4,2, 4, 10; г) 0,6, 3, 2,5, 0,5; д) 0,64, 0.08, 0,8, 2. 223. 1,1; 11,1; 2,2; 2,22; 0,33; 0,333. 224. а) 23 + 2,6 = 2 • 2 • 2 + 2,6 = 8 + 2,6 = 10,6;
225. Число а не кратно числу 3.
226. А(2m); В(2n) или (3m); (7(3n); D(4n) или (6m); координаты точек В и D — общие кратные чисел m и n. 227. Пусть а — длина прямоугольника, b — его ширина. Площадь прямоугольника до увеличения: S1 = а • b. Площадь прямоугольника после увеличения: S2 = (а + 0,3а) • (b + 0,2b); S2 = 1,3а • 1,2b = 1,56 • S1. Если принять S1 за 100%, тогда S2 соответствует 156%, и тогда площадь прямоугольника увеличилась на 156 - 100 = 56%. <<< К началу Решенния (окончание) >>>
|
|
|