Циклические процессы

Циклические газовые процессы состоят из нескольких этапов, причём конечное состояние газа совпадает с начальным. Обычно рассматриваются случаи, когда этапами циклического процесса являются изопроцессы и адиабатный процесс.

Вопросы при этом ставятся, например, такие.

На каких этапах процесса газ получает тепло, а на каких — отдаёт?
Чему равно полученное газом или отданное им количество теплоты?
Чему равно изменение внутренней энергии газа на различных этапах процесса?
Чему равна работа газа за один цикл?
Чему равен КПД цикла?

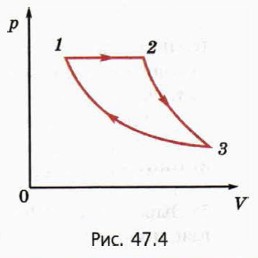
Для простейшего циклического процесса, состоящего из двух изохор и двух изобар, мы уже нашли ответы на эти вопросы (см. § 43). Рассмотрим теперь более сложный цикл.

На рисунке 47.4 изображён график циклического процесса, происходящего с некоторой массой одноатомного идеального газа.

Рис. 47.4

Известно, что при изобарном расширении газ совершает работу А, а при изотермическом сжатии отдаёт холодильнику количество теплоты Q_хол. Требуется найти КПД цикла.

Проанализируем сначала этот циклический процесс качественно. По определению КПД цикла равен отношению работы, совершённой газом за один цикл, к количеству теплоты, переданному газу за этот цикл.

Работа, совершённая газом за один цикл, равна разности работы, совершённой газом при его расширении, и работы, совершённой над газом при его сжатии.

13. На каких этапах процесса газ совершает работу, а на каких этапах работу совершают над газом?

14. На каких этапах процесса газ получает тепло?

Перейдём теперь к количественному описанию. Заметим, что в подобных задачах как работу газа, так и количество теплоты удобно выражать через число молей газа и значения абсолютной температуры газа в различных состояниях газа, даже если эти значения не заданы (в таком случае они сократятся, если найдено правильное решение).

Обозначим T₁, Т₂ и Т₃ значения абсолютной температуры соответственно в состояниях 1, 2, 3. Поскольку процесс 3—1 изотермический, Т₁ = Т₃.

Окончание >>>