|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела Способы описания движения
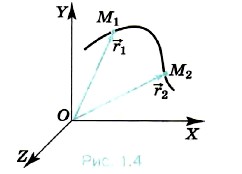
При движении материальной точки радиус-вектор, определяющий её положение, с течением времени изменяется (поворачивается и меняет длину; рис. 1.4), т. е. является функцией времени:
На рисунке 1.4 радиус-вектор
Если оно известно, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение.
Итак, мы знаем, что положение точки в пространстве определяется её координатами или её радиус-вектором. Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось? Изобразим какую-либо ось (рис. 1.5), например ось ОХ. Опустим из начала А и конца В вектора
Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, ах и ау — проекции вектора Согласно определению проекции вектора на ось можно записать: ах = ± |А1В1|.
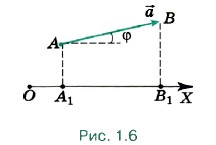
Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора. Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций (рис. 1.6). В противном случае (см. рис. 1.5) она считается отрицательной.
|
|
|



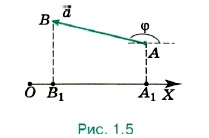
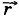 =
= 
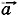 перпендикуляры на ось ОХ. Точки А1 и В1 есть проекции соответственно начала и конца вектора
перпендикуляры на ось ОХ. Точки А1 и В1 есть проекции соответственно начала и конца вектора  В каких случаях проекция вектора на ось максимальна, а в каких — минимальна? Можно ли расположить на плоскости вектор так, чтобы и проекция на ось X, и проекция на ось Y имели максимальные значения?
В каких случаях проекция вектора на ось максимальна, а в каких — минимальна? Можно ли расположить на плоскости вектор так, чтобы и проекция на ось X, и проекция на ось Y имели максимальные значения?