|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 2. Способы описания движения (окончание)Из рисунков 1.5 и 1.6 нетрудно увидеть, что проекция вектора на ось будет положительной, когда вектор составляет острый угол φ с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекции тупой угол φ.
Вопросы к параграфу 1. Какими способами можно задать положение точки? 2. Как задают положение точки в пространстве с помощью координат? 3. Что называется радиус-вектором? 4. Что называется проекцией вектора на ось? 5. Чему равна проекция вектора на ось, если вектор направлен так же, как и ось проекции? 6. Чему равна проекция вектора на ось, если вектор направлен противоположно оси проекции? 7. Чему равна проекция вектора на перпендикулярную к нему ось? Образцы заданий ЕГЭ A1. Точка движется в плоскости XOY. Вектор 1) 0,5; 0,87 2) 0,5; 0 3) 0,87; 0,5 4) 0,87; 0 A2. Точка движется в плоскости XOY. Вектор 1) 1,41; 1,41 2) 0,71; 0 3) -1,41; -0,71 4) -1,41; 1,41 м A3. Начальное положение точки 1) 7 м 2) 5 м 3) 4 м 4) 1 м A4. Начальное положение точки
A5. Точка движется по прямой в плоскости XOY. Начальное положение точки 1) 0° 2) 45° 3) 135° 4) 90°
|
|
|



 Иногда нужно находить составляющие вектора, например векторы
Иногда нужно находить составляющие вектора, например векторы 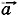 x, и
x, и 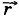 модуль которого равен 1 м, направлен под углом 30° к оси X. Чему равны проекции вектора
модуль которого равен 1 м, направлен под углом 30° к оси X. Чему равны проекции вектора