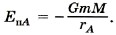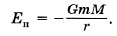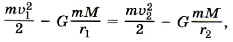|
|
|
|
|
Глава 5. Закон сохранения энергии Работа силы тяготения. Потенциальная энергия в поле тяготенияСуммарная работа силы тяготения при перемещении тела из точки А в точку В равна:
2. При движении тела по траектории АА'В'В (см. рис. 5.15) очевидно, что работа силы тяготения на участках АА' и В'В равна нулю, так как сила тяготения направлена к точке О и перпендикулярна любому малому перемещению по дуге окружности. Следовательно, работа будет также определяться выражением (5.31). 3. Определим работу силы тяготения при движении тела от точки А к точке В по траектории АСВ (см. рис. 5.15). Работа силы тяготения на малом перемещении Δsi равна ΔАi = FсрiΔsicosαi,.. Из рисунка видно, что Δsicosαi = - Δri, и суммарная работа опять же будет определяться по формуле (5.31). Итак, можно сделать вывод, что А1 = А2 = А3, т. е. что работа силы тяготения не зависит от формы траектории. Очевидно, что работа силы тяготения при перемещении тела по замкнутой траектории АА'В'ВА равна нулю.
Изменение потенциальной энергии равно работе силы тяготения, взятой с обратным знаком: Если выбрать нулевой уровень потенциальной энергии на бесконечности, т. е. ЕпВ = 0 при rВ → ∞, то Потенциальная энергия тела массой m, находящегося на расстоянии r от центра Земли, равна:
Закон сохранения энергии для тела массой m, движущегося в поле тяготения, имеет вид
где υ1 — скорость тела на расстоянии r1 от центра Земли, υ2 — скорость тела на расстоянии r2 от центра Земли. Определим, какую минимальную скорость надо сообщить телу вблизи поверхности Земли, чтобы оно в отсутствие сопротивления воздуха могло удалиться от неё за пределы сил земного притяжения.
|
|
|



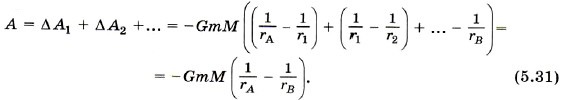
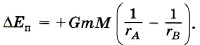
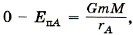 следовательно,
следовательно,