|
|
|
|
|
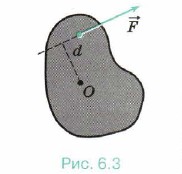
Глава 6. Динамика вращательного движения абсолютно твёрдого тела Основное уравнение динамики вращательного движенияМомент силыДля создания вращательного движения важно не только значение силы, но также и точка её приложения. Отворить дверь, оказывая давление около петель, очень трудно, в то же время вы легко её откроете, надавливая на дверь как можно дальше от оси вращения, например на ручку. Следовательно, для вращательного движения существенно не только значение силы, но и расстояние от оси вращения до точки приложения силы. Кроме этого, важно и направление приложенной силы. Можно тянуть колесо с очень большой силой, но так и не вызвать его вращения.
Очевидно, что момент силы максимален, если сила перпендикулярна радиус-вектору, проведённому от оси вращения до точки приложения этой силы.
При этом моменты сил, вызывающих вращение тела против часовой стрелки, будем считать положительными (сила
Основное уравнение динамики вращательного движения. Подобно тому как опытным путём было показано, что ускорение тела прямо пропорционально действующей на него силе, было установлено, что угловое ускорение прямо пропорционально моменту силы: ε ∼ М. Пусть на материальною точку, движующуюся по окружности, действует сила
mr2ε = М. (6.1) Заметим, что в данном случае r — кратчайшее расстояние от оси вращения до материальной точки и соответственно точки приложения силы.
Таким образом, уравнение (6.1) можно записать в виде Iε = М, откуда
Уравнение (6.2) справедливо и для вращательного движения твёрдого тела, имеющего неподвижную ось вращения, где I — момент инерции твёрдого тела, а М — суммарный момент сил, действующих на тело. В этой главе при расчёте суммарного момента сил мы рассматриваем только силы или их проекции, принадлежащие плоскости, перпендикулярной оси вращения.
|
|
|



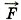 2), а моменты сил, вызывающих вращение по часовой стрелке, — отрицательными (силы
2), а моменты сил, вызывающих вращение по часовой стрелке, — отрицательными (силы 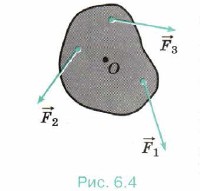

 Понаблюдайте, как человек прикладывает силу к колесу, чтобы раскрутить его.
Понаблюдайте, как человек прикладывает силу к колесу, чтобы раскрутить его.