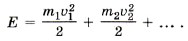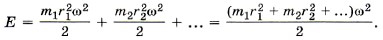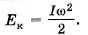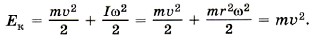Главная >> Физика 10 класс. Мякишев

Глава 6. Динамика вращательного движения абсолютно твёрдого тела

§ 49. Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси (окончание)

Кинетическая энергия вращающегося твёрдого тела

Кинетическая энергия вращающегося твёрдого тела равна сумме кинетических энергий отдельных его частиц. Разделим тело на малые элементы, каждый из которых можно считать материальной точкой. Тогда кинетическая энергия тела равна сумме кинетических энергий материальных точек, из которых оно состоит:

Угловая скорость вращения всех точек тела одинакова, следовательно,

Величина в скобках, как мы уже знаем, это момент инерции твёрдого тела. Окончательно формула для кинетической энергии твёрдого тела, имеющего неподвижную ось вращения, имеет вид

В общем случае движения твёрдого тела, когда ось вращения свободна, его кинетическая энергия равна сумме энергий поступательного и вращательного движений. Так, кинетическая энергия колеса, масса которого сосредоточена в ободе, катящегося по дороге с постоянной скоростью, равна

В таблице сопоставлены формулы механики поступательного движения материальной точки с аналогичными формулами вращательного движения твёрдого тела.

Ключевые слова для поиска информации по теме параграфа. Момент импульса. Энергия вращательного движения. Гироскоп

Вопросы к параграфу

1. Что характеризует момент инерции тела?

2. В каком случае справедлив закон сохранения момента импульса?

3. Массы и радиусы диска и кольца равны между собой. Оси вращения проходят через центры кольца и диска. Момент инерции какого тела больше кольца или диска?

4. С одной и той же высоты с наклонной плоскости скатывается диск и соскальзывает брусок. Скорость какого тела будет больше? Считайте, что работа силы трения мала.

5. В течение 0,1 с по касательной к ободу вращающегося колеса действовала сила, равная 10 Н. Чему равно изменение момента импульса колеса?

<<< К началу