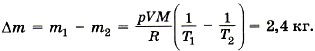|
|
|
|
|
Глава 10. Уравнение состояния идеального газа. Газовые законы
§ 64. Примеры решения задач по теме «Уравнение состояния идеального газа»При решении задач по данной теме надо чётко представлять себе начальное состояние системы и какой процесс переводит её в конечное состояние. Одна из типичных задач на использование уравнения состояния идеального газа: требуется определить параметры системы в конечном состоянии по известным макроскопическим параметрам в её начальном состоянии. Задача1. Воздух состоит из смеси газов (азота, кислорода и т. д.). Плотность воздуха ρ0 при нормальных условиях (температура t0 = 0 °С и атмосферное давление р0 = 101 325 Па) равна 1,29 кг/м3. Определите среднюю (эффективную) молярную массу М воздуха. Р е ш е н и е. Уравнение состояния идеального газа при нормальных условиях имеет вид
Задача2. Определите температуру кислорода массой 64 г, находящегося в сосуде объёмом 1 л при давлении 5 • 106 Па. Молярная масса кислорода М = 0,032 кг/моль. Р е ш е н и е. Согласно уравнению Менделеева—Клапейрона Отсюда температура кислорода Задача3. Определите плотность азота при температуре 300 К и давлении 2 атм. Молярная масса азота М = 0,028 кг/моль. Р е ш е н и е. Запишем уравнение Менделеева—Клапейрона: Разделив на объём левую и правую части равенства, получим
Задача4. Определите, на сколько масса воздуха в комнате объёмом 60 м3 зимой при температуре 290 К больше, чем летом при температуре 27 °С. Давление зимой и летом равно 105 Па. Р е ш е н и е. Запишем уравнение Менделеева—Клапейрона: Из этого уравнения выразим массу газа: Таким образом,
|
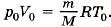Здесь R = 8,31 Дж/(моль • К) и Т0 = 0 °С + 273 °С = 273 К, М — эффективная молярная масса воздуха. Эффективная молярная масса смеси газов — это молярная масса такого воображаемого газа, который в том же объёме и при той же температуре оказывает на стенки сосуда то же давление, что и смесь газов, в данном случае воздух. Отсюда
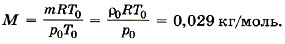
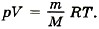
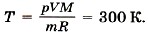
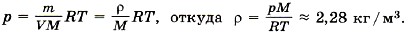
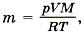где T принимает значения Т1 и Т2 — температуры воздуха зимой и летом. Молярная масса воздуха М = 0,029 кг/моль. Температура воздуха летом Т2 = 27 °С + 273 °С = 300 К.
|
|