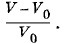Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев

Глава 3. Температура. Газовые законы

§ 3.6. Закон Гей-Люссака. Идеальный газ

Сообщение об открытии еще одного газового закона было опубликовано лишь в 1802 г., спустя почти 150 лет после открытия закона Бойля—Мариотта. Закон, определяющий зависимость объема газа от температуры при постоянном давлении (и неизменной массе), был установлен французским ученым Гей-Люссаком (1778—1850).

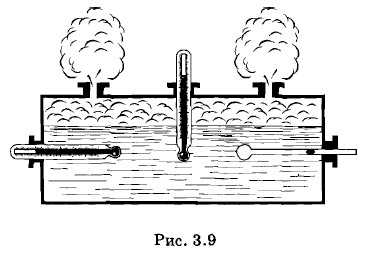
Закон Гей-Люссака, Изобары, Идеальный газ, Газовая шкала температур

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (от греческих слов: isos — равный и baros — тяжесть, вес).

Схематически прибор Гей-Люссака показан на рисунке 3.9. Исследуемый газ находится в стеклянном баллончике, соединенном с длинной стеклянной трубкой. Газ заперт небольшой капелькой ртути в трубке. Так как трубка расположена горизонтально, то давление в баллончике все время остается равным атмосферному. Температура газа с помощью специального нагревателя увеличивается от 0 до 100 °С. За изменением объема можно следить по перемещению капельки ртути.

При изучении теплового расширения следует рассматривать не абсолютное изменение объема, а относительное. Если при температуре t₀ = 0 °С объем газа равен V₀, а при температуре t он равен V, то относительное изменение объема есть

На основании наблюдений Гей-Люссак установил закон: относительное изменение объема газа данной массы при постоянном давлении прямо пропорционально изменению температуры t;

где α — температурный коэффициент объемного расширения.

Температурный коэффициент объемного расширения а численно равен относительному изменению объема газа при изменении его температуры на 1 °С.

Измеряя объем газа при двух опорных точках, например 0 и 100 °С, можно найти коэффициент α:

при условии, что р₁₀₀ = р₀.

Опыт показывает, что при малых плотностях температурный коэффициент объемного расширения одинаков для всех газов:

Это означает, что газы изменяют свой объем примерно на 1/273 того объема, который каждый из газов занимал при 0 °С, если температура меняется на 1 °С.

С точки зрения молекулярно-кинетической теории, одинаковое значение коэффициента а для всех газов объясняется тем, что молекулы газа находятся в среднем на больших по сравнению с их размером расстояниях друг от друга. Особенности межмолекулярных сил для различных газов в этих условиях не сказываются.

Уравнение (3.6.1) можно записать в другой форме:

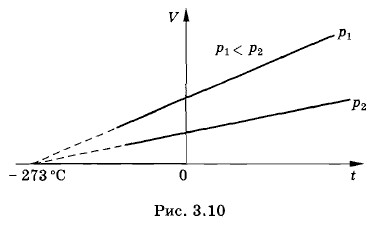
Объем газа определенной массы согласно уравнению (3.6.4) при постоянном давлении меняется линейно при изменении температуры.

Экспериментальное определение зависимости объема газа от температуры

Убедиться в справедливости закона Гей-Люссака можно с помощью уже известного нам прибора (см. рис. 3.7). Для этого, заметив показания манометра, следует измерить температуру газа в гофрированном сосуде и объем сосуда. Затем нужно нагреть газ, поместив сосуд в горячую воду, и, вращая винт, добиться того, чтобы показания манометра остались прежними. Снова измерить температуру и объем газа. После этого опять изменить температуру, добиться первоначального значения давления и измерить температуру и объем газа в третий раз.

Изобары

Используя найденные значения объема газа при различных температурах и одном и том же давлении, можно построить график зависимости V от t. Эта зависимость изобразится прямой линией — изобарой, как и должно быть согласно формуле (3.6.4).

Различным давлениям соответствуют разные изобары (рис. 3.10). Так как с ростом давления объем газа при постоянной температуре уменьшается (закон Бойля—Мариотта), то изобара, соответствующая более высокому давлению р₂, лежит ниже изобары, соответствующей более низкому давлению р₁.

Идеальный газ

Если продолжить изобары в область низких температур, где измерения не проводились, то все прямые пересекают ось температуры в точке, соответствующей объему, равному нулю (пунктирные прямые на рис. 3.10). Но это не означает, что объем газа действительно обращается в нуль. Ведь все газы при сильном охлаждении превращаются в жидкости, а к жидкостям ни закон Гей-Люссака, ни закон Бойля—Мариотта неприменимы.

Реальные газы подчиняются основным газовым законам лишь приближенно и тем менее точно, чем больше плотность газа и ниже его температура. Газ, который в точности подчиняется газовым законам, называют идеальным.

Газовая шкала температур

Тот факт, что численное значение температурного коэффициента объемного расширения в предельном случае малых плотностей одинаково для всех газов, позволяет установить температурную шкалу, не зависящую от вещества, — идеальную газовую шкалу температур.

Приняв за основу шкалу Цельсия, можно определить температуру из соотношения (3.6.1)

где V₀ — объем газа при 0 °С, а V — его объем при температуре t.

Таким образом, с помощью формулы (3.6.5) осуществляется определение температуры, не зависящее от вещества термометра.

Дано определение идеального газа как газа, в точности подчиняющегося законам Бойля—Мариотта и Гей-Люссака. Введена идеальная газовая шкала температур, не зависящая от вещества.