|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 3. Температура. Газовые законы § 3.9. Уравнение состояния идеального газа
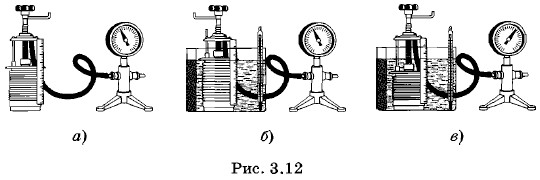
Уравнение состоянияВ § 3.5 и 3.6 вы ознакомились с поведением идеального газа в специально созданных условиях. Два параметра из трех (р, V или V, Т) изменялись при постоянном значении третьего (Т или р). Обычно же в природе и технике у газа меняются сразу все три параметра. Например, когда нагретый у поверхности Земли воздух поднимается вверх, то он расширяется, давление его уменьшается и температура понижается. Используя газовые законы (3.5.2) и (3.7.8), можно получить уравнение, связывающее все три параметрар, V и Т, характеризующие состояние газа данной массы. Это уравнение называют уравнением состояния идеального газа. Изменение состояния газаДля опыта используем уже известный нам прибор (см. рис. 3.7). Пусть в начальном состоянии 1 газ в сосуде (рис. 3.12, а) имеет давление р1, объем V1 и температуру Т1, равную температуре окружающего воздуха. Затем газ переходит в конечное состояние 2, при котором давление, объем и температура будут иметь значения р2, V2, Т2. Какова связь между всеми этими величинами?
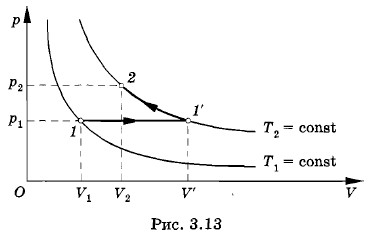
Переведем газ из состояния 1 в состояние 2 с помощью двух процессов, подчиняющихся законам Гей-Люссака и Бойля— Мариотта: изобарного и изотермического. Для этого поместим сосуд в большую банку с водой, нагретой до температуры Т2 (рис. 3.12, б). Вода в банке будет служить термостатом. Одновременно начнем увеличивать объем газа так, чтобы давление р1 оставалось постоянным (изобарный процесс). Газ с течением времени перейдет в промежуточное состояние 1' с объемом V' и температурой Т2. Графически этот переход изобразится прямой 1—1' на рисунке 3.13.
Затем изотермически при температуре Т2 переведем газ в конечное состояние с давлением р2 и объемом V2, медленно уменьшая объем сосуда (рис. 3.12, в). Графически это изобразится участком гиперболы 1'—2 (см. рис. 3.13). Вывод уравнения состояния идеального газаСогласно закону Гей-Люссака (3.7.8)
Применяя закон Бойля—Мариотта (3.5.2) для изотермического процесса, получим p1V'=p2V2. (3.9.2) Выразим из уравнения (3.9.1) V':
и подставим полученное значение в уравнение (3.4.2), тогда
В пределах точности, обеспечиваемой экспериментальной установкой, данный результат согласуется с опытом. Так как начальное и конечное состояния газа выбраны произвольно, то произведение давления газа данной массы на его объем, деленное на абсолютную температуру, есть величина постоянная, не зависящая от состояния, в котором находится газ:
Уравнение (3.9.5) носит название уравнения Клапейрона* и представляет собой одну из форм записи уравнения состояния идеального газа. * Б. П. Клапейрон (1799—1864) — французский физик, в течение 10 лет работал в России. Если величина Универсальная газовая постояннаяВозьмем вначале газ в количестве 1 моль, его объем обозначим через VM. При температуре 0 °С и атмосферном давлении 101 325 Па объем моля любого газа один и тот же: VМО = 0,0224 м3/моль. Следовательно, для моля любого газа
Таким образом, для одного моля газа произведение давления на объем, отнесенное к абсолютной температуре, является постоянной величиной для всех газов. Эту постоянную называют универсальной газовой постоянной и обозначают буквой R: R = 8,31 Дж/(моль • К). (3.9.6) Уравнение Менделеева—КлапейронаДля 1 моль идеального газа, как вытекает из выражений (3.9.5) и (3.9.6), pVM = RT. (3.9.7)
Пусть теперь количество газа равно не 1 моль, а произвольному числу молей
Умножая обе части уравнения (3.9.7) на v и учитывая уравнение (3.9.8), получим наиболее общую формулу уравнения состояния для произвольной массы идеального газа
В такой форме уравнение состояния было впервые записано великим русским ученым Д. И. Менделеевым. Поэтому уравнение (3.9.9) называют уравнением Менделеева — Клапейрона. Единственная величина в уравнении состояния, зависящая от рода газа, это его молярная масса.
|
|
|





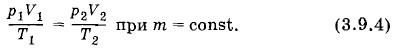

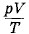 постоянна, то естественно выяснить, чему равна эта постоянная.
постоянна, то естественно выяснить, чему равна эта постоянная.
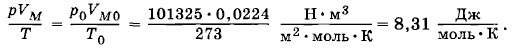

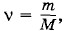 где m — масса газа, а М — его молярная масса. Объем V этого количества вещества при тех же значениях давления и температуры равен
где m — масса газа, а М — его молярная масса. Объем V этого количества вещества при тех же значениях давления и температуры равен

