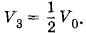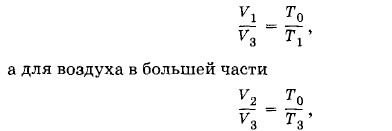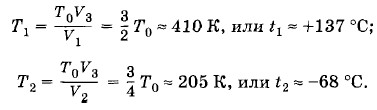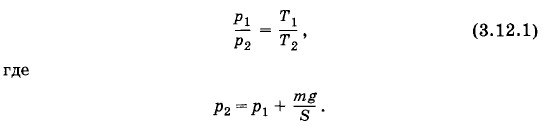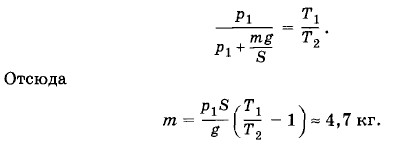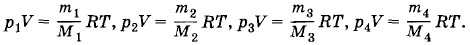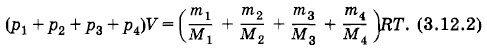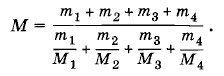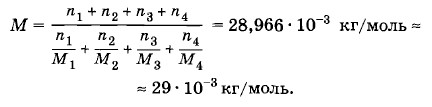|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 3. Температура. Газовые законы Примеры решения задач на темы: Температура. Газовые законыЗадачи на применение газовых законов очень разнообразны. Для их решения нельзя указать какой-либо один определенный прием. Полезными могут оказаться следующие советы. 1. Если согласно условию задачи один из трех параметров (р, V или Т) постоянный, то при Т = const надо применять закон Бойля—Мариотта (3.5.2), при р = const — закон Гей-Люссака (3.7.7), а при V = const — закон Шарля (3.10.2) или (3.10.3). 2. Если изменяются все три параметра, то следует воспользоваться уравнением состояния в форме (3.9.9) или (3.9.5). Уравнение состояния (3.9.9) применяется в тех случаях, когда известна масса газа и часть макроскопических параметров в определенном состоянии газа и надо найти неизвестные величины. 3. Для определения давления смеси газов, не вступающих в химические реакции, используют закон Дальтона (3.8.2). 4. Во многих задачах требуется построение графиков, изображающих разного рода процессы. Для этого нужно знать зависимость параметров друг от друга, которая в общем случае дается уравнением состояния, а в частных — газовыми законами. 5. При решении большинства задач надо четко представлять себе, каково начальное состояние системы и какой процесс переводит его в конечное состояние. Задача 1Как измерить медицинским термометром температуру тела человека, если температура окружающего воздуха +42 °С? Решение. Можно предварительно охладить термометр в холодильнике. Если холодильника нет, то нужно подержать термометр 5—8 мин под мышкой, извлечь его и сразу же стряхнуть. Термометр покажет температуру тела, так как ртуть в термометре сожмется при контакте с телом до объема, соответствующего температуре тела. Задача 2Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу т и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно р. Определите давление газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной. Решение. При горизонтальном положении цилиндра объем каждой его части обозначим через V (эти объемы равны). При вертикальном положении цилиндра объем верхней части станет равным V + ΔV, а нижней V - ΔV. Давление в нижней части цилиндра станет равным
Исключив из этих равенств
Второй корень квадратного уравнения отрицателен и потому лишен физического смысла. Задача 3Поршневой насос при каждом качании захватывает воздух объемом V0. При откачке этим насосом воздуха из сосуда объемом V насос совершил п качаний. Затем другой насос с тем же рабочим объемом V0 начал нагнетать воздух из атмосферы в тот же сосуд, совершив также п качаний. Какое давление установится в сосуде? Температуру воздуха во время работы насоса считать постоянной. Решение. Согласно закону Бойля—Мариотта при откачке воздуха из сосуда после первого качания давление в сосуде станет равным При нагнетании воздуха в сосуд после n качаний давление станет равным
При любом n р > р0, так как во время нагнетания воздуха при каждом качании насос захватывает воздух, имеющий атмосферное давление р0, а при откачке при каждом качании удаляется воздух при давлении, меньшем р0. Задача 4В запаянной с обоих концов цилиндрической трубке находится воздух при нормальных условиях. Трубка разделена подвижным поршнем на две части, объемы которых V1 и V2 относятся как 1 : 2. До какой температуры t1 следует нагреть воздух в меньшей части трубки и до какой t2 охладить в большей, чтобы поршень делил трубку на две равные части, если нагревание и охлаждение в обеих частях трубки производятся при условии Решение. Условие Согласно закону Гей-Люссака для воздуха в меньшей части трубки выполняется соотношение
где Т0 = 273 К — температура, соответствующая начальным условиям. Отсюда
Задача 5В цилиндре под поршнем находится воздух при давлении p1 = 2 • 105 Па и температуре t1 = 27 °С. Определите массу т груза, который нужно положить на поршень после нагревания воздуха до температуры t2 = 50 °С, чтобы объем воздуха в цилиндре стал равен первоначальному. Площадь поршня S = 30 см2. Решение. Так как в процессе нагревания объем воздуха в цилиндре не изменяется, то согласно закону Шарля имеем Решение. Так как в процессе нагревания объем воздуха в цилиндре не изменяется, то согласно закону Шарля имеем
Подставляя в (3.12.1) выражение для р2, получим
Задача 6Найдите среднюю (эффективную) молярную массу сухого атмосферного воздуха, предполагая известный процентный состав воздуха по массе: азот — n1 = 75,52%, кислород — n2 = 23,15%, аргон — n3 = 1,28% и углекислый газ— n4 = 0,05%. Решение. Для каждого газа можно записать уравнение состояния:
Здесь M1, M2, M3 и M4 — молярные массы соответственно азота, кислорода, аргона и углекислого газа. Складывая правые и левые части этих уравнений, получим
Для смеси газов выполняется соотношение
где m = m1 + m2 + m3 + m4 — масса воздуха с объемом V, а М — искомая эффективная молярная масса. Согласно закону Дальтона p = p1 + p2 + p3 + p4. Сравнивая уравнения состояния (3.12.2) и (3.12.3), получим
Разделив числитель и знаменатель на т и умножив на 100%, получим выражение для М через процентный состав воздуха по массе
Примеры решения задач (окончание) >>>
|
|
|



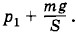 Согласно закону Бойля—Мариотта
Согласно закону Бойля—Мариотта
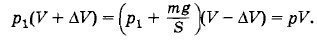
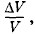 получим квадратное уравнение для p1:
получим квадратное уравнение для p1:
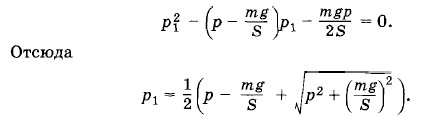
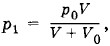 где р0 — атмосферное давление. После второго качания будет выполняться равенство р2V = p2(V + V0) и, следовательно,
где р0 — атмосферное давление. После второго качания будет выполняться равенство р2V = p2(V + V0) и, следовательно, 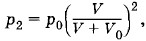 и т. д. После n качании в сосуде установится давление
и т. д. После n качании в сосуде установится давление 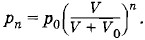
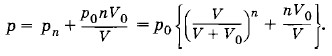
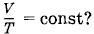
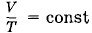 означает, что процессы нагревания и охлаждения происходят изобарно. При отношении начальных объемов
означает, что процессы нагревания и охлаждения происходят изобарно. При отношении начальных объемов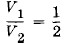 эти объемы составляют
эти объемы составляют 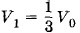 и
и  где V0 — объем всей трубки. Конечные объемы обеих частей одинаковы и равны
где V0 — объем всей трубки. Конечные объемы обеих частей одинаковы и равны