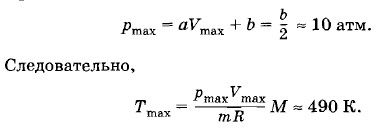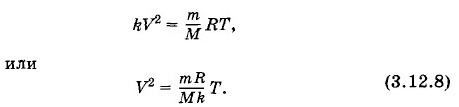|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 3. Температура. Газовые законы Примеры решения задач на темы: Температура. Газовые законыЗадача 7Закрытый с обоих концов цилиндр наполнен газом при давлении р — 100 кПа и температуре t = 30 °С и разделен подвижным теплонепроницаемым поршнем на две равные части длиной L по 50 см. На какую величину ΔТ нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние l = 20 см, если во второй половине цилиндра температура не изменяется? Определите давление газа после смещения поршня. Решение. Для газа в части цилиндра с постоянной температурой применим закон Бойля—Мариотта: pLS = p1(L - l)S, (3.12.4) где S — площадь основания цилиндра. Для нагреваемой части цилиндра запишем уравнение Клапейрона:
В уравнениях (3.12.4) и (3.12.5)р1 — давление газа после смещения поршня, одинаковое в обеих частях цилиндра вследствие равновесия поршня, а Т + ΔТ в уравнении (3.12.5) — температура газа в нагретой части цилиндра. Разделив почленно уравнение (3.12.4) на уравнение (3.12.5), получим
Из уравнения (3.12.4) находим р1.
Задача 8Сосуд объемом V = 100 л разделен пополам полупроницаемой перегородкой. В начальный момент времени в одной половине сосуда находился водород, масса которого m1 = 2 г, а во второй — 1 моль азота. Определите давления, установившиеся по обе стороны перегородки, если она может пропускать только водород. Температура в обеих половинах одинакова и постоянна: t = 127 °С. Решение. Так как водород свободно проходит через перегородку, то он распространяется по всему сосуду. Запишем уравнение Менделеева—Клапейрона для водорода после установления состояния равновесия:
где M1 = 2 • 10-3 кг/моль — молярная масса водорода. В той части сосуда, в которой вначале был только водород, он и в дальнейшем останется в чистом виде, так что давление в этой части сосуда станет равным
Для азота уравнение Менделеева—Клапейрона имеет вид
где р2 — давление азота. Так как в этой половине находятся водород и азот, то полное давление р согласно закону Дальтона складывается из парциальных давлений р1 и р2, т. е.
Задача 9
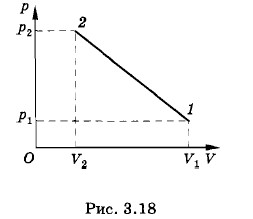
Гелий массой 20 г, заключенный в теплоизолированном цилиндре под поршнем, медленно переводится из состояния 1 с объемом V1 = 32 л и давлением р1 = 4,1 атм в состояние 2 с объемом V2 = 9 л и давлением р2 = 15,5 атм. Какой наибольшей температуры достигнет газ при этом процессе, если на графике зависимости давления газа от объема процесс изображается прямой линией (рис. 3.18)? Решение. Как следует из рисунка 3.18, давление и объем газа связаны линейной зависимостью: р = aV + b, где а и b — постоянные коэффициенты. Из условий задачи получаем систему уравнений p1 = aV1 + b, р2 = аV2 + b. Решив эту систему относительно а и b, найдем
Подставив в уравнение Менделеева—Клапейрона вместо р выражение aV + b, получим
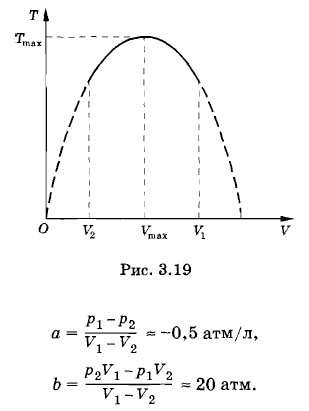
График зависимости Т от V представляет собой параболу (рис. 3.19). Кривая достигает максимума при При этом
Задача 10
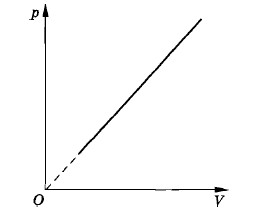
На рисунке 3.20 изображен график изменения состояния идеального газа в координатах р, V. Начертите графики этого процесса в координатах V, Т и р, Т. Решение. Из рисунка 3.20 следует, что давление газа р и его объем V находятся в прямой пропорциональной зависимости p = kV, (3.12.7) где k — постоянный коэффициент. Подставив значение давления (3.12.7) в уравнение Менделеева— Клапейрона, получим
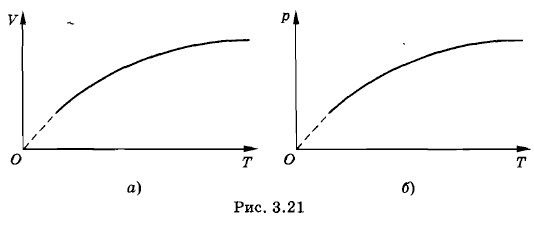
Уравнение (3.12.8) — это уравнение параболы, ось симметрии которой совпадает с осью Т. Следовательно, в координатах V, Т искомый график имеет вид, показанный на рисунке 3.21, а. Аналогично получим график этого процесса в координатах р, Т (рис. 3.21,6).
|
|
|



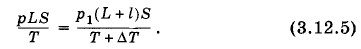
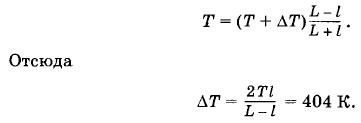
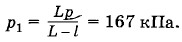
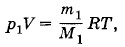
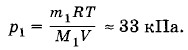
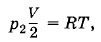
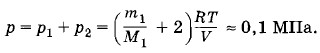
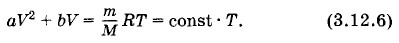
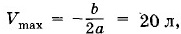 когда корни квадратного уравнения (3.12.6) совпадают.
когда корни квадратного уравнения (3.12.6) совпадают.