|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
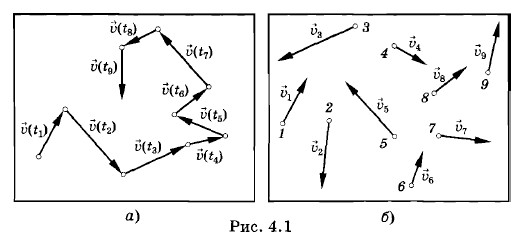
Глава 4. Молекулярно-кинетическая теория идеального газа Системы с большим числом частиц и законы механики. Статистическая механикСтатистическая механикаТрудности создания количественной теории процессов, происходящих внутри макроскопических тел, на основе представления о движении молекул кажутся на первый взгляд непреодолимыми. Однако задача исследования систем из огромного числа частиц все же поддается решению. Поведение таких систем обнаруживает определенные закономерности. Но это уже закономерности нового типа, закономерности статистической механики, или статистической физики. Оказывается, что для описания свойств макроскопических тел и процессов с их участием, которые наблюдаются на опыте, не нужно знать микроскопическое состояние системы (значения всех координат и импульсов частиц). Важно знать не поведение отдельных молекул, а средний результат, к которому приводит их совокупное движение. Этот средний результат и можно предвидеть с помощью законов статистической механики. Очевидно, каждому микроскопическому состоянию отвечает определенное макроскопическое состояние (определенные значения макроскопических параметров). Однако одному и тому же макроскопическому состоянию может отвечать огромное число микроскопических состояний. Например, ни давление, ни температура газа в состоянии термодинамического равновесия не меняются, но молекулы, из которых состоит газ, непрерывно движутся, микроскопические состояния системы непрерывно сменяют друг друга. Средние по времени и статистические средниеПеред статистической механикой стоит задача определения средних значений любых функций координат и скоростей молекул без вычисления зависимости этих величин от времени. Посмотрим, как в принципе можно решить эту задачу на примере вычисления среднего значения квадрата скорости Υ2 молекулы газа, от которого зависит ее средняя кинетическая энергия Допустим, что в сосуде с газом, температура которого поддерживается постоянной, имеется достаточно большое число N молекул. Выделим мысленно одну из них. Если произвести ряд последовательных измерений скорости данной молекулы в моменты времени t1, t2, t3 и т. д. через малые одинаковые промежутки времени (рис. 4.1, а), проделав достаточно большое число N1 измерений (в принципе это возможно), то среднее по времени значение квадрата скорости можно записать так:
Это простое арифметическое среднее. Далее очевидно, что все N молекул газа находятся в одинаковых макроскопических условиях. Ни одна из них не выделяется в смысле характера своего поведения среди других. Поэтому средний квадрат скорости газовой молекулы можно определить и по-другому. Пусть одновременно измерены скорости Υ1, Υ2, ..., ΥN всех молекул (рис. 4.1, б). Тогда средний квадрат скорости молекулы равен среднему арифметическому квадратов скоростей всех молекул газа в данный момент:
Определенное так среднее значение квадрата скорости Основное допущение, которое принимается в статистической механике, состоит в том, что среднее по времени совпадает со статистическим средним. В рассмотренном простом случае такое допущение представляется достаточно естественным. Оно предполагает полный хаос в движении молекул, когда все они в общем ведут себя одинаково. Теория строится так, чтобы она позволяла определять статистические средние, так как задача непосредственного вычисления временных средних заведомо невыполнима. Два этапа становления статистической механики (молекулярно-кинетической теории)В первых исследованиях принималось в качестве приближения, что все молекулы имеют одинаковые модули скоростей, равные их средним значениям. С помощью этих средних скоростей вычислялось среднее число соударений молекул в секунду, средняя длина свободного пробега и т. д. Решительный шаг вперед был сделан в 1859 г. английским физиком Дж. Максвеллом (1831—1879), который впервые ввел в физику понятие вероятности, выработанное ранее при анализе азартных игр. До Максвелла казалось, что единственной альтернативой предположения о равенстве скоростей их средним значениям является строгое решение уравнений Ньютона для всех частиц системы. Введение вероятности позволило наряду со средними значениями физических величин рассматривать вероятности того, что эти величины принимают те или иные значения. В дальнейшем понятие вероятности стало основным для любого статистического закона. Мы в основном ограничимся знакомством с элементарными вычислениями средних значений. Лишь во второй части главы на простом примере познакомимся с вероятностными законами статистической механики.
|
|
|



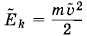 (знак «~» сверху означает усреднение по времени).
(знак «~» сверху означает усреднение по времени).
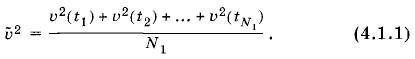
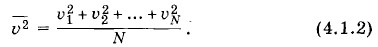
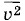 называется статистическим средним (или средним по совокупности) в отличие от среднего по времени значения квадрата скорости
называется статистическим средним (или средним по совокупности) в отличие от среднего по времени значения квадрата скорости