|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 4. Молекулярно-кинетическая теория идеального газа § 4.8. Внутренняя энергия идеального газа
Наиболее прост по своим свойствам одноатомный газ, т. е. газ, состоящий из отдельных атомов, а не молекул. Одноатомными являются инертные газы — гелий, неон, аргон и др. Можно получить одноатомный (атомарный) водород, кислород и т. д. Однако такие газы будут неустойчивыми, так как при столкновениях атомов образуются молекулы Н2, 02 и др. Молекулы идеального газа не взаимодействуют друг с другом, кроме моментов непосредственного столкновения. Поэтому их средняя потенциальная энергия очень мала и <i>вся энергия представляет собой кинетическую энергию хаотического движения молекул. Это, конечно, справедливо, если сосуд с газом покоится, т. е. газ как целое не движется (его центр масс находится в покое). В этом случае упорядоченное движение отсутствует и механическая энергия газа равна нулю. Газ обладает энергией, которую называют внутренней. Для вычисления внутренней энергии идеального одноатомного газа массой т нужно умножить среднюю энергию одного атома, выражаемую формулой (4.5.5), на число атомов. Это число равно произведению количества вещества Умножая выражение (4.5.5) на
Внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре. От объема газа она не зависит. Внутренняя энергия газа представляет собой среднюю кинетическую энергию всех его атомов. Если центр масс газа движется со скоростью υ0, то полная энергия газа равна сумме механической (кинетической) энергии
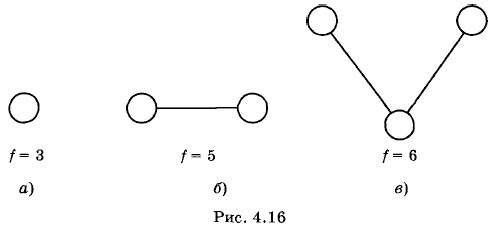
Внутренняя энергия молекулярных газовВнутренняя энергия одноатомного газа (4.8.1)— это по существу средняя кинетическая энергия поступательного движения молекул. В отличие от атомов молекулы, лишенные сферической симметрии, могут еще вращаться. Поэтому наряду с кинетической энергией поступательного движения молекулы обладают и кинетической энергией вращательного движения. В классической молекулярно-кинетической теории атомы и молекулы рассматриваются как очень маленькие абсолютно твердые тела. Любое тело в классической механике характеризуется определенным числом степеней свободы ƒ — числом независимых переменных (координат), однозначно определяющих положение тела в пространстве. Соответственно число независимых движений, которые тело может совершать, также равно ƒ. Атом можно рассматривать как однородный шарик с числом степеней свободы ƒ = 3 (рис. 4.16, а). Атом может совершать только поступательное движение по трем независимым взаимно перпендикулярным направлениям. Двухатомная молекула обладает осевой симметрией (рис. 4.16, б) и имеет пять степеней свободы. Три степени свободы соответствуют ее поступательному движению и две — вращательному вокруг двух осей, перпендикулярных друг другу и оси симметрии (линии, соединяющей центры атомов в молекуле). Многоатомная молекула, подобно твердому телу произвольной формы, характеризуется шестью степенями свободы (рис. 4.16, в); наряду с поступательным движением молекула может совершать вращения вокруг трех взаимно перпендикулярных осей.
От числа степеней свободы молекул зависит внутренняя энергия газа. Вследствие полной беспорядочности теплового движения ни один из видов движения молекулы не имеет преимущества перед другим. На каждую степень свободы, соответствующую поступательному или вращательному движению молекул, приходится одна и та же средняя кинетическая энергия. В этом состоит теорема о равномерном распределении кинетической энергии по степеням свободы (она строго доказывается в статистической механике). Средняя кинетическая энергия поступательного движения молекул равна
Если эту величину умножить на число степеней свободы и число молекул газа массой m, то получится внутренняя энергия произвольного идеального газа:
Эта формула отличается от формулы (4.8.1) для одноатомного газа заменой множителя 3 на множитель ƒ.
|
|
|



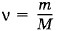 на постоянную Авогадро NA.
на постоянную Авогадро NA.
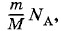 получим внутреннюю энергию идеального одноатомного газа:
получим внутреннюю энергию идеального одноатомного газа:

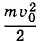 и внутренней энергии U:
и внутренней энергии U:
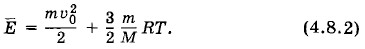
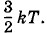 Поступательному движению соответствуют три степени свободы. Следовательно, средняя кинетическая энергия
Поступательному движению соответствуют три степени свободы. Следовательно, средняя кинетическая энергия 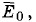 приходящаяся на одну степень свободы, равна
приходящаяся на одну степень свободы, равна

