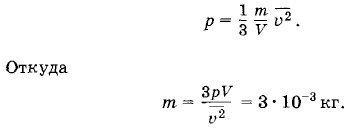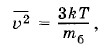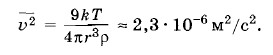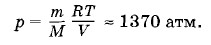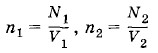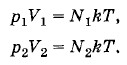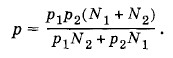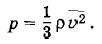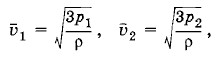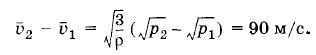|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 4. Молекулярно-кинетическая теория идеального газа Примеры решения задач на тему: Молекулярно-кинетическая теория идеального газаПри решении задач на применение молекулярно-кинетической теории идеального газа используются основное уравнение кинетической теории газов в форме (4.4.9) или (4.4.10) и вытекающие из него выражения для средней кинетической энергии молекул (4.5.5) и средней квадратичной скорости (4.7.2) или (4.7.3). Значительное количество задач удобно решать, используя формулу (4.5.6), связывающую давление газа с концентрацией молекул и абсолютной температурой. Внутренняя энергия идеальных одноатомных газов (например, инертных газов) вычисляется по формуле (4.8.1). Задача 1Чему равна масса газа, содержащегося в закрытом цилиндре вместимостью V = 0,5 л, если давление газа р = 5 • 105 Па, а средняя квадратичная скорость молекул Решение. Согласно основному уравнению молекулярнокинетической теории
где ρ = m0n — плотность газа. Но
Задача 2В воздухе при t = 27 °С взвешены пылинки сферической формы. Радиус пылинок r = 10-6 м. Плотность вещества пылинок ρ = 1,3 • 103 кг/м3. Определите средний квадрат скорости пылинок. Решение. Пылинки принимают участие в броуновском движении. Средний квадрат скорости пылинки
где m6 — масса пылинки. Следовательно,
Задача 3В сосуде находится 1 л воды при температуре 27 °С. Каким стало бы давление внутри сосуда, если бы силы взаимодействия между молекулами внезапно исчезли? Решение. При исчезновении сил взаимодействия между молекулами вода превратилась бы в идеальный газ. Давление можно найти по уравнению состояния идеального газа:
Задача 4Два сосуда, содержащих различные газы, соединены трубкой с краном. Давление газа в первом сосуде p1, а число молекул N1. Давление газа во втором сосуде р2, число молекул N2. Какое давление установится в сосудах, если открыть кран соединительной трубки? Температуру считать постоянной. Решение. Согласно формуле (4.5.6) р1 = n1kТ и р2 = n2kT, где
(здесь V1 и V2 — объемы сосудов). Следовательно,
После того как кран будет открыт, давления выравняются и искомое давление согласно той же формуле (4.5.6) определится уравнением p(V1 + V2) = (N1+ N2)kT. Подставляя сюда выражения для объемов из предыдущих формул, получим
Задача 5Плотность газа в баллоне газополной электрической лампы ρ = 0,9 кг/м3. При горении лампы давление в ней возросло с р1 = 8 • 104 Па до р2 = 1,1 • 105 Па. На сколько увеличилась при этом средняя квадратичная скорость молекул? Решение. Плотность газа ρ = m0n, и основное уравнение молекулярно-кинетической теории можно записать в форме
Поэтому
откуда
|
|
|



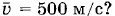
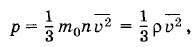
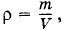 где m — масса газа, а V — его объем. Поэтому
где m — масса газа, а V — его объем. Поэтому