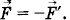|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 5. Законы термодинамики § 5.1. Работа в термодинамикеТепловые явления можно описывать с помощью величин (макроскопических параметров), регистрируемых такими приборами, как манометр и термометр. Эти приборы не реагируют на воздействие отдельных молекул. Теория тепловых процессов, в которой не учитывается молекулярное строение тел, называется термодинамикой. Об этом уже упоминалось в главе 1. В этой главе термодинамику мы будем изучать.
Работа в механике и термодинамикеВ механике рассматривается движение макроскопических тел. Работа определяется как произведение модулей силы и перемещения и косинуса угла между направлениями силы и перемещения. Работа совершается при действии силы или нескольких сил на движущееся макроскопическое тело и равна изменению его кинетической энергии. В термодинамике движение тела как целого не рассматривается и речь идет о перемещении частей макроскопического тела друг относительно друга. При совершении работы меняется объем тела, а его скорость остается равной нулю. Но скорости молекул тела, например газа, меняются. Поэтому меняется и температура тела. Причина состоит в следующем: при упругих соударениях молекул с движущимся поршнем (для случая сжатия газа) их кинетическая энергия изменяется. Так, при движении навстречу молекулам поршень во время столкновений передает им часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги и сообщающему мячу скорость, значительно большую той, которой он обладал до удара*. * Задача об изменении скорости шарика при упругом соударении его с движущейся стенкой подробно рассмотрена в § 6.12 «Механики» (задача 5). И наоборот, если газ расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует футболист: чтобы уменьшить скорость летящего мяча или остановить его, нога футболиста движется от мяча, как бы уступая ему дорогу. Итак, при совершении работы в термодинамике меняется состояние макроскопических тел: меняется их объем и температура. Вычисление работыВычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем (рис. 5.1). Проще всего вначале вычислить не работу силы
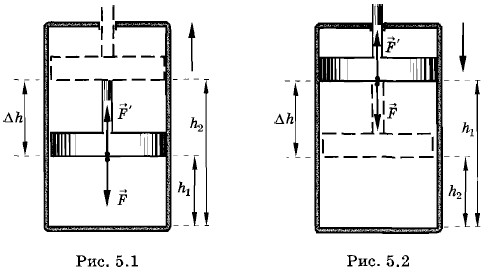
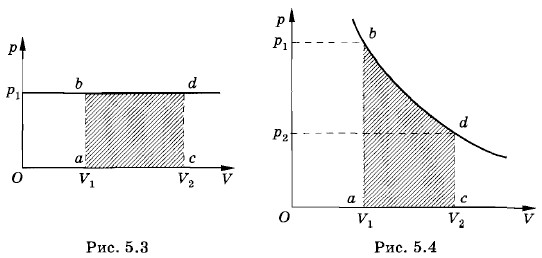
Модуль силы, действующей со стороны газа на поршень, равен F' = pS, где р — давление газа, a S — площадь поверхности поршня. Пусть газ расширяется и поршень смещается в направлении силы на малое расстояние Δh = h2 - h1 Если перемещение мало́, то давление газа можно считать постоянным. Работа газа равна А' = F' Δh = pS(h2 - h1) = p(Sh2 - Sh1). (5.1.1) Эту работу можно выразить через изменение объема газа. Начальный объем V1 = Shlt а конечный V2 = Sh2. Поэтому A' = p(V2 - V1) = pΔV, где ΔV = V2 - V1 — изменение объема газа. При расширении газ совершает положительную работу, так как направления силы и перемещения поршня совпадают. Если газ сжимается, то формула (5.1.2) для работы газа остается справедливой. Но теперь V2 < V1, и поэтому А' < 0 (рис. 5.2). Работа А, совершаемая внешними телами над газом, отличается от работы газа А' только знаком: А = -А', так как сила A = -A' = -pΔV. (5.1.3) Знак минус указывает, что при сжатии газа, когда ΔV = V2 — V1 < 0, работа внешней силы положительна. Понятно, почему в этом случае А > 0: при сжатии газа направления силы и перемещения совпадают. При расширении газа, наоборот, работа внешних тел отрицательна (А < 0), так как ΔV = V2 - V1 > 0. Теперь направления силы и перемещения противоположны . Выражения (5.1.2) и (5.1.3) справедливы не только при сжатии или расширении газа в цилиндре, но и при малом изменении объема любой системы. Если процесс изобарный (р = const), то эти формулы можно применять и для больших изменений объема. Геометрическое истолкование работыРаботе газа А' для случая постоянного давления можно дать простое геометрическое истолкование. Построим график зависимости давления газа от объема (рис. 5.3). Здесь площадь прямоугольника abcd, ограниченная графиком p1 = const, осью V и отрезками аb и cd, равными давлению газа, численно равна работе (5.1.2).
В общем случае при произвольном изменении объема газа давление не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему (рис. 5.4). В этом случае для вычисления работы нужно общее изменение объема разделить на малые части, вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему будет численно равна площади фигуры, ограниченной графиком зависимости р от V, осью V и отрезками ab и cd, равными давлениям р1 и р2 в начальном и конечном состояниях.
|
|
|



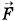 , действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сам газ, действуя нашоршень с силой
, действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сам газ, действуя нашоршень с силой 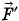 . Согласно третьему закону Ньютона
. Согласно третьему закону Ньютона