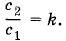Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев

Глава 5. Законы термодинамики

§ 5.2. Количество теплоты

При совершении работы происходит перемещение макроскопических тел, например перемещение поршня при сжатии газа, рассмотренном в предыдущем параграфе. При таком перемещении изменяется состояние газа. Но изменить состояние тела можно без совершения работы, простым нагреванием.

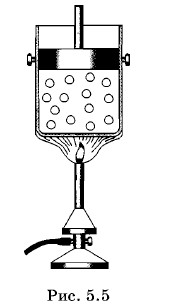
Состояние газа в цилиндре будет меняться, если поршень закрепить и нагревать газ при помощи горелки (рис. 5.5). Объем газа при этом не меняется, но температура и давление увеличиваются. В таких случаях говорят, что системе передано некоторое количество теплоты. Это есть второй способ изменения состояния тел.

Термин «количество переданной теплоты» или, короче, «количество теплоты» возник в те времена, когда тепло рассматривалось как неуничтожимая жидкость — теплород, способная перетекать от тела с большей температурой к телу с меньшей температурой. Считалось, что чем больше в теле теплорода, тем выше его температура, а количество теплоты, переданной телу, понимали как количество перетекшего к нему теплорода.

В действительности, как мы теперь хорошо знаем, никакой неуничтожимой жидкости — теплорода — не существует. Нагревание тела означает увеличение скоростей его молекул. При взаимодействии медленных молекул холодной системы с более быстрыми молекулами горячей на границе систем происходит выравнивание кинетических энергий молекул. В результате скорости молекул холодной системы увеличиваются, а горячей — уменьшаются.

Калориметрические опыты

Подобно тому как изобретение термометра позволило дать определение температуры, понятие количества теплоты приобрело точный смысл после изобретения калориметра — прибора, в котором можно наблюдать теплообмен между телами, изолированными от взаимодействия с окружающей средой.

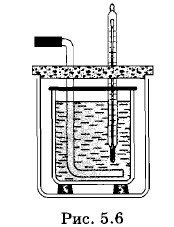
Возьмем большой тонкостенный металлический сосуд, имеющий форму стакана. Этот стакан поставим на кусочки пробки внутрь другого, большего стакана так, чтобы между стаканами оставался слой воздуха. Сверху закроем оба сосуда крышкой (рис. 5.6). Это несложное устройство и представляет собой калориметр. Он сконструирован так, чтобы максимально уменьшить теплообмен содержимого внутреннего стакана с внешней средой.

Нальем в калориметр воду, масса которой m₁ и температура t₁ а затем добавим в него воды массой m₂ и температурой t₂. Пусть t₂ > t₁ В сосуде начнется теплообмен, и спустя некоторое время установится состояние теплового равновесия — обе порции воды примут одинаковую температуру t. Очевидно, t₁ < t < t₂.

Изменение состояния обеих порций воды можно отнести за счет того, что первая порция получила некоторое количество теплоты, а вторая его отдала. Часть теплоты будет передана стенкам самого калориметра. Но если его масса во много раз меньше масс m₁ и m₂, то можно пренебречь нагревом сосуда, не допустив при этом большой ошибки.

Как видите, опыт крайне прост. Но понадобилось немало остроумия и настойчивости, чтобы с помощью этого и подобных ему опытов обнаружить сохранение новой, неизвестной ранее величины. Прежде всего было замечено, что для данных масс воды m₁ и m₂ при любых значениях начальных температур t₁ и t₂ выполняется замечательное по своей простоте равенство:

Причем заметьте, никто не знал, что должна существовать какая-либо простая связь между изменениями температур и массами. В нахождении подобных простых связей и заключается одна из сторон таланта ученого. Располагая калориметром, вы сами легко можете убедиться в справедливости равенства (5.2.1). Существенно, что формула (5.2.1) выполняется не только для воды, но и для любой жидкости.

Теперь усложним опыт. Вместо второй порции воды опустим в калориметр кусок железа массой m₂, температура которого t₂ > t₁. С течением времени опять установится равновесное состояние. Но связь между температурами и массами будет иной. В правой части выражения (5.2.1) появится коэффициент k:

Этот коэффициент можно определить, измерив t и зная t₁, t₂, m₁ и m₂. Его значение остается неизменным при любых массах и начальных температурах веществ. Но если взять вместо железа алюминий или вместо воды масло, то значение этого коэффициента будет другим. Отсюда можно сделать вывод, что конечная температура в калориметре зависит не только от масс m₁ и m₂ веществ, но еще от специфических тепловых свойств самих веществ. Эту зависимость и характеризует коэффициент k.

Так как для одинаковых веществ k = 1, то этот коэффициент можно записать в виде отношения величин с₂ и c₁, характеризующих тепловые свойства веществ (например, железа и воды). Наряду с отношением масс 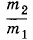в правой части равенства (5.2.2) должно стоять отношение

Окончание параграфа >>>