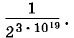|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 5. Законы термодинамики Статистическое истолкование необратимости процессов в природеРасширение «газа» из четырех молекулРассмотрим простой пример, позволяющий вычислить вероятности различных состояний и наглядно показывающий, как увеличение числа частиц в системе приводит к тому, что процессы становятся необратимыми, несмотря на обратимость законов движения микрочастиц.
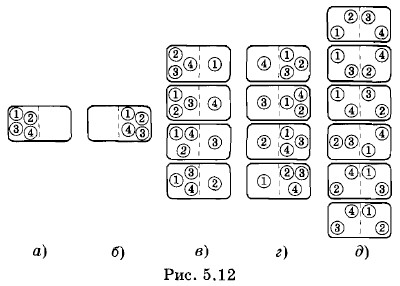
Пусть у нас имеется «газ» в сосуде, состоящий всего лишь из четырех молекул. Вначале все молекулы находятся в левой половине сосуда, отделенной перегородкой от правой половины (рис. 5.12, а). Уберем перегородку, и «газ» начнет расширяться, занимая весь сосуд. Посмотрим, какова вероятность того, что «газ» опять сожмется, т. е. молекулы снова соберутся в одной половине сосуда. В нашем примере макросостояние будет характеризоваться указанием числа молекул в одной половине сосуда безотносительно к тому, какие именно молекулы здесь находятся. Микросостояния задаются распределением молекул по половинам сосуда с указанием того, какие именно молекулы занимают данную половину сосуда. Пронумеруем молекулы цифрами 1, 2, 3, 4. Возможны 16 различных микросостояний, все они изображены на рисунке 5.12, а — д. Вероятность того, что все молекулы соберутся в одной половине (например, левой) сосуда, равна
так как данному макросостоянию соответствует одно микросостояние (см. рис. 5.12, а, б). Вероятность же того, что молекулы распределятся поровну, будет в 6 раз больше:
так как данному макросостоянию соответствует шесть микросостояний (см. рис. 5.12, д). Вероятность того, что в одной половине сосуда (например, левой) будет три молекулы (а в другой соответственно одна молекула), равна (см. рис. 5.12, в, г)
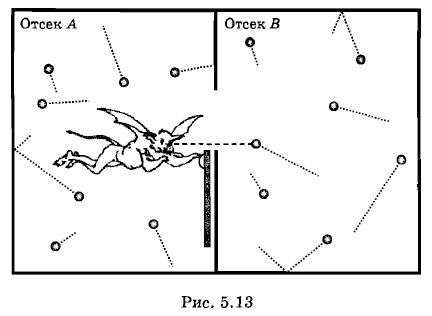
Бо́льшую часть времени молекулы будут распределены по половинам сосуда поровну: это наиболее вероятное состояние. Но примерно Необратимость расширения газа с большим числом молекулНо эта обратимость возможна лишь при небольшом числе молекул. Если же число молекул становится огромным, то результат существенно меняется. Подсчитаем вероятность события, когда молекулы вновь соберутся в одной половине сосуда после расширения, если число молекул произвольно. Молекулы идеального газа практически движутся независимо друг от друга. Для одной молекулы вероятность того, что она окажется в левой половине сосуда, равна, очевидно, Но если взять реальное число молекул газа в 1 см3 при нормальных условиях (n = 3 • 1019), то вероятность того, что молекулы соберутся в одной половине сосуда объемом 1 см3, будет совершенно ничтожна: Таким образом, только из-за большого числа молекул в макротелах процессы в природе оказываются практически необратимыми. В принципе обратные процессы возможны, но вероятность их близка к нулю. Не противоречит, строго говоря, законам природы процесс, в результате которого при случайном движении молекул все они соберутся в одной половине класса, а учащиеся в другой половине класса задохнутся. Но реально это событие никогда не происходило в прошлом и не произойдет в будущем. Слишком мала вероятность подобного события, чтобы оно когда-либо случилось за все время существования Вселенной в современном состоянии — около нескольких миллиардов лет. По данным оценкам, эта вероятность примерно такого же порядка, как и вероятность того, что 20 000 обезьян, хаотически ударяя по клавишам пишущих машинок, напечатают без единой ошибки «Войну и мир» Л. Н. Толстого. В принципе это возможно, но реально никогда не произойдет. Стрела времениВо всех процессах существует выделенное направление, в котором процессы идут сами собой от более упорядоченного состояния к менее упорядоченному. Чем больше порядок в системе, тем сложнее восстановить его из беспорядка. Несравненно проще разбить стекло, чем изготовить новое и вставить его в раму. Гораздо проще убить живое существо, чем возвратить его к жизни, если это вообще возможно. «Бог сотворил маленькую букашку. Если ты ее раздавишь, она умрет» — такой эпиграф поставил американский биохимик Сент Дьерди к своей книге «Биоэнергетика». Выделенное направление времени («стрела времени»), воспринимаемое нами, очевидно, связано именно с направленностью процессов в мире. Границы применимости второго закона термодинамикиВероятность обратных процессов перехода от равновесных состояний к неравновесным для макроскопических систем в целом очень мала. Но для малых объемов, содержащих небольшое число молекул, вероятность отклонения от равновесия становится заметной. Такие случайные отклонения от равновесия называются флуктуациями. Именно флуктуациями плотности газа в областях порядка длины световой волны объясняется рассеяние света в атмосфере Земли и голубой цвет неба. Флуктуации давления в малых объемах объясняют броуновское движение. Наблюдение флуктуаций служит важнейшим доказательством правильности созданной Больцманом статистической теории необратимости макропроцессов. Второй закон термодинамики выполняется только для систем с огромным числом частиц. В малых объемах становятся существенными отклонения от этого закона. «Демон Максвелла»Любопытный пример якобы возможного нарушения второго закона термодинамики придумал Максвелл. Разумное существо — «демон» — управляет очень легкой заслонкой в перегородке, разделяющей два отсека — А и Б — с газом, находящимся при одинаковой температуре и давлении (рис. 5.13). «Демон» следит за молекулами, подлетающими к заслонке, и открывает ее только для быстрых молекул, движущихся из отсека В в отсек А. В результате с течением времени газ в отсеке А нагревается, а в отсеке В остывает. Работа при этом не совершается, так как заслонка практически невесома, и второй закон термодинамики как будто нарушается.
Однако в действительности нарушения второго закона не происходит. Для своей работы «демон» должен получать информацию о скоростях подлетающих к заслонке молекул. Получить же такую информацию без затрат энергии невозможно. Для получения такой информации надо, к примеру, направлять на молекулы электромагнитное излучение и принимать отраженные сигналы.
|
|
|



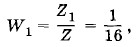
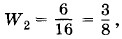
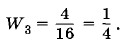
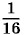 достаточно большого интервала времени наблюдения молекулы будут занимать одну из половин сосуда. Таким образом, процесс расширения обратим и «газ» снова сжимается через сравнительно небольшой промежуток времени.
достаточно большого интервала времени наблюдения молекулы будут занимать одну из половин сосуда. Таким образом, процесс расширения обратим и «газ» снова сжимается через сравнительно небольшой промежуток времени.
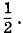 Такова же вероятность и для другой молекулы. Эти события независимы, и вероятность того, что первая и вторая молекулы соберутся в левой половине сосуда, равна произведению вероятностеи:
Такова же вероятность и для другой молекулы. Эти события независимы, и вероятность того, что первая и вторая молекулы соберутся в левой половине сосуда, равна произведению вероятностеи: 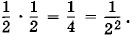 Для трех молекул вероятность нахождения молекул в одной половине сосуда равна
Для трех молекул вероятность нахождения молекул в одной половине сосуда равна 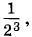 а для четырех —
а для четырех — 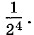 Именно такое значение вероятности мы и получили при детальном рассмотрении распределения молекул по сосуду.
Именно такое значение вероятности мы и получили при детальном рассмотрении распределения молекул по сосуду.