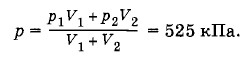|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 5. Законы термодинамики Примеры решения задач на тему: Законы термодинамикиПри решении задач на применение материала этой главы используется формула (5.1.2) или (5.1.3) для вычисления работы при изобарном изменении объема газа, выражение (5.2.5) для количества теплоты, полученного телом при его нагревании или отданного им при охлаждении, а также уравнение теплового баланса (5.2.6). Значительное количество задач решается с помощью первого закона термодинамики в форме ΔU = А + Q или Q = ΔU + А'. Надо иметь в виду, что величины A, Q и ΔU могут быть как положительными, так и отрицательными. В ряде случаев используются частные формулировки первого закона термодинамики для изотермического, изобарного, изохорного и адиабатного процессов. При решении задач на тепловые двигатели применяются выражения для КПД (5.11.2) и (5.12.13). Во многих случаях понадобится применять газовые законы и выражение для внутренней энергии одноатомного идеального газа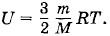
Задача1Вычислите работу идеального газа массой m при его изобарном нагревании на ΔТ. Решение. Обозначим постоянное давление газа через р, начальный и конечный объемы газа — соответственно через V1 и V2, а начальную и конечную температуры — через Т1 и Т2. Согласно уравнению Менделеева—Клапейрона имеем
Задача 2В каком случае вода в бадье нагревается больше: при опускании в нее горячего камня или такого же по объему нагретого до той же температуры куска металла? Удельные теплоемкости камня и металла относятся как 2:1, плотности как 3:13. Решение. Пренебрегая тепловыми потерями, запишем уравнения теплового баланса для двух пар веществ: вода — камень и вода — металл:
Задача 3После опускания в воду, имеющую температуру t1 = 10 °С, тела, нагретого до температуры t2 = 100 °С, через некоторое время установилась общая температура t = 40 °С. Какой станет температура воды t', если, не вынимая первого тела, в нее опустить еще одно такое же тело, нагретое тоже до температуры t2 = 100 °С? Решение. Пренебрегая нагреванием сосуда и тепловыми потерями, запишем уравнение теплового баланса после опускания первого тела:свтв (t - t1) + cTmT (t - t2) = 0, (5.13.6) Преобразуем уравнения (5.13.6) и (5.13.7) так:
Задача 4В цилиндре под тяжелым поршнем, перемещающимся без трения, находится углекислый газ массой m = 20 г. Газ нагревается от температуры t1 = 20 °С до температуры t2 = 108 °С. Какое количество теплоты было при этом сообщено газу? Молярная теплоемкость углекислого газа (теплоемкость 1 моль) при постоянном объеме CV = 28,8 Дж/(К • моль). Решение. Молярная теплоемкость при постоянном давлении согласно формуле (5.6.7) равнаСр = CV + R. Удельная теплоемкость
Задача 5В двух цилиндрах, имеющих объемы V1 = 3 л и V2 = 5 л, находится одинаковый газ при давлениях р1 = 0,4 МПа и р2 = 0,6 МПа и температурах t1 = 27 °С и t2 = 127 °С. Цилиндры соединяют трубкой с краном. Определите, какая температура Т и какое давление р установятся в цилиндрах после того, как кран соединительной трубки будет открыт. Решение. Внутренние энергии газа в первом цилиндре, газа во втором цилиндре и газа в цилиндрах после смешивания соответственно равны U1 = bν1T1, U2 = bν2T2 и U = b(ν1 + ν2)T. Здесь b — коэффициент пропорциональности, зависящий от природы газа (для одноатомного газа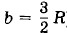 ); ν1 — число молей газа в первом цилиндре; ν2 — число молей газа во втором цилиндре.
Согласно закону сохранения энергии ); ν1 — число молей газа в первом цилиндре; ν2 — число молей газа во втором цилиндре.
Согласно закону сохранения энергии
U = U1 + U2, (5.13.11) или ν1T1 + ν2T2 = (ν1 + ν2)T. (5.13.12) Отсюда
p(V1 + V2) = (ν1 + ν2)RT, используя найденные значения для ν1, ν2 и Т, получим
Примеры решения задач (окончание) >>>
|
|
|



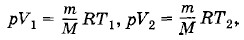 где М — молярная масса газа.
Вычитая почленно из второго уравнения первое, получим
где М — молярная масса газа.
Вычитая почленно из второго уравнения первое, получим
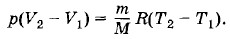 Ho p(V2 - V1) = А' — работа газа. Следовательно,
Ho p(V2 - V1) = А' — работа газа. Следовательно,
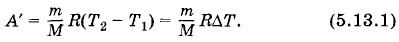 Полученную формулу полезно запомнить и применять при решении других задач.
Полученную формулу полезно запомнить и применять при решении других задач.
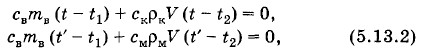 где св, ск, см— удельные теплоемкости воды, камня и металла; mв— масса воды в бадье; ρк и ρм — плотности камня и металла; V — объем камня (металла); t1 — начальная температура воды в бадье; t2 — начальная температура камня (металла); t — температура, установившаяся в бадье после опускания в нее камня, a t' — после опускания металла.
Перепишем уравнения (5.13.2) так:
где св, ск, см— удельные теплоемкости воды, камня и металла; mв— масса воды в бадье; ρк и ρм — плотности камня и металла; V — объем камня (металла); t1 — начальная температура воды в бадье; t2 — начальная температура камня (металла); t — температура, установившаяся в бадье после опускания в нее камня, a t' — после опускания металла.
Перепишем уравнения (5.13.2) так:
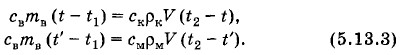 Разделив почленно первое уравнение на второе, получим
Разделив почленно первое уравнение на второе, получим
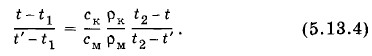 Так как
Так как 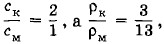 то уравнение (5.13.4) принимает вид
то уравнение (5.13.4) принимает вид
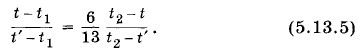 Относительно температур t и t' можно высказать три предположения: 1) t > t'; 2) t = t' и 3) t < t'.
В первом случае в уравнении (5.13.3) левая часть больше единицы, а правая меньше. Значит, первое предположение несправедливо. Во втором случае (t = t') левая часть уравнения (5.13.5) равна единице, а правая равна
Относительно температур t и t' можно высказать три предположения: 1) t > t'; 2) t = t' и 3) t < t'.
В первом случае в уравнении (5.13.3) левая часть больше единицы, а правая меньше. Значит, первое предположение несправедливо. Во втором случае (t = t') левая часть уравнения (5.13.5) равна единице, а правая равна 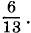 Следовательно, неверно и второе предположение.
Таким образом, правильным является третье утверждение: t < t', т. е. при опускании металла вода нагреется больше.
Следовательно, неверно и второе предположение.
Таким образом, правильным является третье утверждение: t < t', т. е. при опускании металла вода нагреется больше.
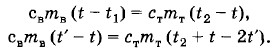 После почленного деления второго уравнения на первое получим
После почленного деления второго уравнения на первое получим
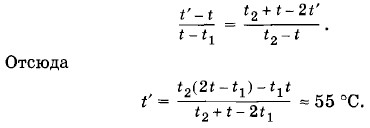
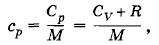 где М — молярная масса газа.
Следовательно, искомое количество теплоты
где М — молярная масса газа.
Следовательно, искомое количество теплоты
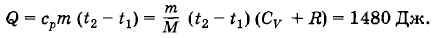
 Из уравнений состояния до смешивания газов следует
Из уравнений состояния до смешивания газов следует
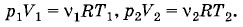 Выразим отсюда количества газов:
Выразим отсюда количества газов:
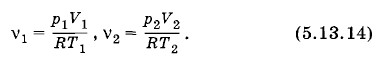 Подставив значения ν1 и ν2 в формулу (5.13.13), получим
Подставив значения ν1 и ν2 в формулу (5.13.13), получим
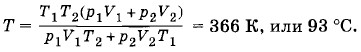 Из уравнения состояния для смеси газов
Из уравнения состояния для смеси газов