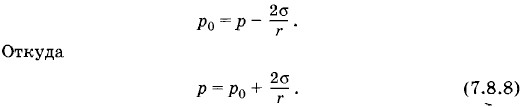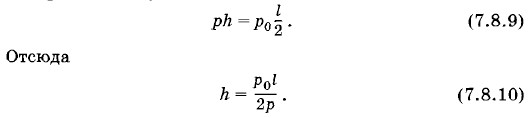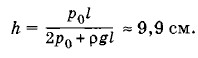|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 7. Поверхностное натяжение в жидкостях Примеры решения задач на тему: Поверхностное натяжение в жидкостяхЗадача 4
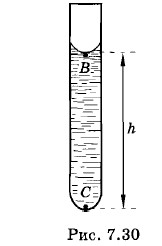
Длинную стеклянную капиллярную трубку, радиус канала которой r = 1 мм, закрыли снизу и наполнили водой. Трубку поставили вертикально и открыли ее нижний конец, при этом часть воды вылилась. Какова высота столба оставшейся в капилляре воды? Решение. Столб воды в поставленной вертикально трубке удерживается верхним и нижним менисками (рис. 7.30). Давление в точке В под верхним мениском
Задача 5Конец капиллярной трубки опущен в воду. Какое количество теплоты Q выделится при поднятии жидкости по капилляру? Краевой угол принять равным нулю (полное смачивание). Решение. Жидкость поднимается согласно формуле (7.7.3) на высоту
Силы поверхностного натяжения совершают работу
На увеличение потенциальной энергии Ер идет половина этой работы. Следовательно, выделение теплоты происходит за счет другой половины. Таким образом,
Задача 6Капиллярная трубка погружена в воду таким образом, что длина непогруженной ее части составляет l = 0,2 м. Вода поднялась в трубке на высоту Решение. Согласно формуле (7.7.3)
Найдем давление воздуха, которое установится в погруженном закрытом сверху капилляре после выравнивания уровней воды (в сосуде и капилляре). Обозначим давление воздуха в капилляре буквой р, тогда под вогнутой поверхностью
воды в капилляре давление равно
Полагая температуру неизменной и применив закон Бойля—Мариотта, получим
Найдем из уравнения (7.8.7) значение σ и подставим его в выражение (7.8.8):
И наконец, подставив в (7.8.10) выражение (7.8.11) для р, окончательно получим
|
|
|



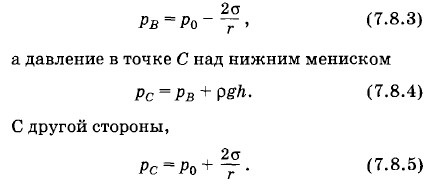
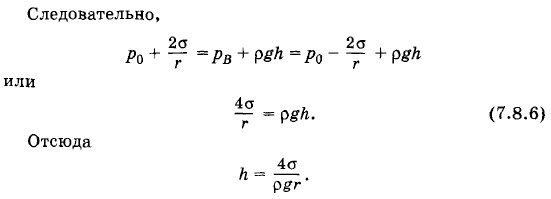
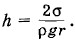 Потенциальная энергия столбика жидкости в поле тяготения Земли
Потенциальная энергия столбика жидкости в поле тяготения Земли
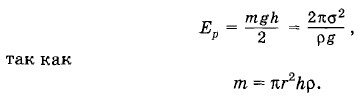
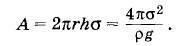
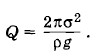
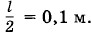 В этом положении верхний конец трубки закрывают пальцем и трубку погружают в воду до тех пор, пока уровень воды в ней не сравняется с уровнем воды в сосуде. Найдите длину выступающей из воды части трубки в этом положении. Внешнее давление р0 = 105 Па.
В этом положении верхний конец трубки закрывают пальцем и трубку погружают в воду до тех пор, пока уровень воды в ней не сравняется с уровнем воды в сосуде. Найдите длину выступающей из воды части трубки в этом положении. Внешнее давление р0 = 105 Па.

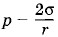 (см. § 7.6). Так как жидкость в капилляре и сосуде находится в равновесии, то давление на жидкость в сосуде (атмосферное давление р0) равно давлению
(см. § 7.6). Так как жидкость в капилляре и сосуде находится в равновесии, то давление на жидкость в сосуде (атмосферное давление р0) равно давлению