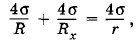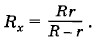|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 7. Поверхностное натяжение в жидкостях Примеры решения задач на тему: Глава 7. Поверхностное натяжение в жидкостяхЗадачи на материал данной главы отличаются от обычных задач на гидростатику лишь тем, что в них принимается во внимание еще одна сила — сила поверхностного натяжения, определяемая формулой (7.4.3). Для решения задач используются также формулы для поверхностной энергии (7.3.2), давления под изогнутой поверхностью (7.6.6) и высоты поднятия жидкости в капилляре (7.7.3). Задача 1Определите энергию, освободившуюся при слиянии мелких капель воды радиусом r = 2 • 10-3 мм в одну большую каплю радиусом R = 2 мм. Считать, что при слиянии мелких капель температура не изменяется. Поверхностное натяжение воды равно σ = 7,4 • 10-2 Н/м. Решение. Обозначим число мелких капель через п. Тогда общая поверхность всех мелких капель S1 = 4πr2n. Поверхность одной большой капли S2 = 4πR2. Поверхностная энергия всех мелких капель Uп1 = σ • 4πr2n, а одной крупной капли Uп2 = σ • 4πR2. Так как температура не изменялась, то кинетическая энергия молекул воды тоже не изменилась. Следовательно, выделение энергии произошло за счет уменьшения потенциальной (поверхностной)энергии: Q = Uп1 - Uп2 = 4πσ(r2n - R2). (7.8.1) Чтобы найти число капель n, учтем, что объем воды не изменился. Сумма объемов мелких капель
Подставляя это значение n в выражение (7.8.1), получим
Задача 2Смачиваемый водой кубик массой m = 0,02 кг плавает на поверхности воды. Ребро кубика имеет длину а = 0,03 м. На каком расстоянии х от поверхности воды находится нижняя грань кубика? Решение. Архимедова сила уравновешивает силу тяжести кубика и силу поверхностного натяжения. Следовательно,
Силы поверхностного натяжения вносят поправку около 1 мм. Задача 3
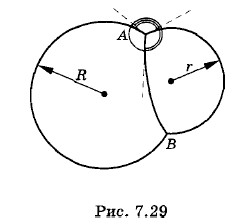
Два мыльных пузыря радиусами R и r «срослись», как показано на рисунке 7.29. Какую форму примет пленка, разделяющая оба пузыря? Какие углы образуются между пленками в местах их соприкосновения? Решение. Давление внутри мыльного пузыря радиусом R больше атмосферного давления на величину
где Rx — радиус кривизны участка пленки АВ. Отсюда
Силы поверхностного натяжения в любой точке поверхности соприкосновения пузырей уравновешивают друг друга и равны между собой. А это возможно только в том случае, когда углы между векторами сил равны 120°.
|
|
|




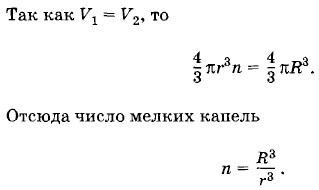
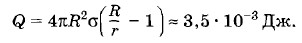
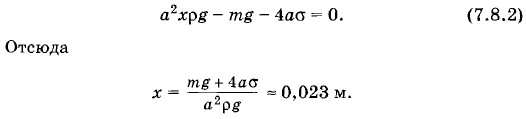
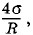 а внутри меньшего пузыря — на величину
а внутри меньшего пузыря — на величину 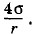 В этих выражениях учтено, что у мыльного пузыря две поверхности. Давление внутри пузыря радиусом R вместе с давлением участка пленки между пузырями должно уравновесить давление внутри меньшего пузыря. Следовательно,
В этих выражениях учтено, что у мыльного пузыря две поверхности. Давление внутри пузыря радиусом R вместе с давлением участка пленки между пузырями должно уравновесить давление внутри меньшего пузыря. Следовательно,