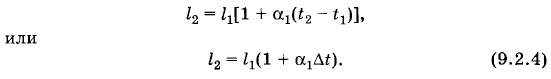|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 9. Тепловое расширение твердых и жидких тел § 9.2. Тепловое линейное расширение
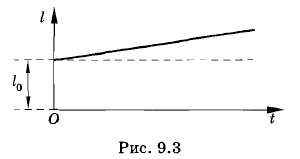
Опыт показывает, что при небольших изменениях температуры изменение линейных размеров твердого тела прямо пропорционально изменению температуры (рис. 9.3). Так как удлинение при нагревании (или укорочение при охлаждении) зависит также от первоначальной длины тела, удобнее рассматривать не само удлинение тела, а относительное удлинение: отношение увеличения длины ωl = l - l0 к первоначальной длине l0. Относительное удлинение
Коэффициент пропорциональности α1 называют температурным коэффициентом линейного расширения. Он показывает, на какую долю своего первоначального значения изменяются линейные размеры тела при нагревании его на 1 К. Коэффициент линейного расширения зависит от природы вещества, а также от температуры. Однако, если рассматривать изменения температуры в не слишком широких пределах, зависимостью α1 от температуры можно пренебречь и считать температурный коэффициент линейного расширения величиной постоянной для данного вещества. Для большинства веществ этот коэффициент мал, его значения составляют 10-5—10-6К-1. Особенно мал коэффициент линейного расширения в диапазоне температур от -30 до +100 °С у инвара (сплав железа и никеля). Поэтому инвар применяют для изготовления точных инструментов, используемых при определении размеров тел. Линейные размеры самого инструмента из инвара мало зависят от колебаний температуры. Линейные размеры тела, как вытекает из формулы (9.2.1), зависят от изменения температуры следующим образом: l = l0(1 + α1Δt). (9.2.2) В формулах (9.2.1) и (9.2.2) обычно начальное значение температуры полагают равным нулю (t0 = 0 °С) и соответственно t0 считают длиной тела при этой температуре. На практике же начальная температура тела далеко не всегда бывает равна 0 °С. Тогда расчет длины тела при любой температуре можно выполнить так. Пусть при температуре t1 длина тела равна l1, а при температуре t2 она равна l2. Тогда, считая начальную температуру t0 = 0 °С, имеем l1 = l0(1 + α1t1),
Отсюда
Однако, учитывая, что значение α1 очень мало, формулу (9.2.3) можно упростить. Умножив числитель и знаменатель на 1 - α1t1, получим
Ввиду малости коэффициента α1 члены, содержащие
Решая задачи с учетом теплового линейного расширения тел, необходимо иметь в виду, что при изменении температуры меняется не только длина, но и все другие линейные размеры тела. Так, у круглого стержня при нагревании увеличивается диаметр, и притом во столько раз, во сколько увеличивается длина стержня. У пластинки в одно и то же число раз увеличиваются длина, ширина и толщина. Если начертить на пластинке какую-нибудь линию, то длина этой линии при нагревании увеличится в такое же число раз. У окружности увеличатся ее длина и диаметр. При нагревании пластинки, имеющей круглое отверстие, диаметр отверстия тоже увеличится. Дело в том, что при равномерном нагревании в теле не возникают силы упругости. Поэтому расширение происходит так, как если бы пластинка была сплошной. Точно так же увеличивается при нагревании диаметр гайки, размеры раковины в толще металлической отливки и т. д. В справедливости сказанного можно убедиться на опыте с металлическим шаром, о котором уже шла речь в § 9.1. Шар застревает в кольце, если его нагреть, и проходит с большим зазором, если нагреть кольцо. Наоборот, при охлаждении кольца шар застревает, а охлаждение шара увеличивает зазор между ним и кольцом.
|
|
|



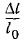 пропорционально изменению температуры ωt = t - t0:
пропорционально изменению температуры ωt = t - t0:

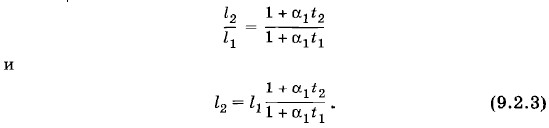
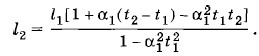
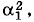 малы по сравнению с членом, в который входит α1 в первой степени (точнее,
малы по сравнению с членом, в который входит α1 в первой степени (точнее, 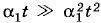 ). Поэтому их можно отбросить. В результате формула для вычисления длины l2 оказывается более простой и достаточно точной для инженерной практики:
). Поэтому их можно отбросить. В результате формула для вычисления длины l2 оказывается более простой и достаточно точной для инженерной практики: