|
|
|
|
|
§ 3. Сила Лоренца Модуль силы Лоренца (окончание)За время t через поперечное сечение проводника пройдёт заряд Q = Nq, (5) где N число свободных зарядов в этом проводнике, q — величина каждого из них. Подставив в формулу (3) выражения (4) и (5), получим:
Подставим теперь это выражение для силы тока в формулу (2) для силы Ампера. Мы получим FА = NBqυ. (6) Учтём теперь, что сила Ампера действует на все N свободных зарядов в проводнике, а сила Лоренца — только на один заряд. Следовательно,
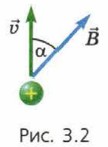
Из формул (6) и (7) следует, что FЛ = Bqυ. Доказательство завершено. Подобным же образом можно доказать, что если скорость заряженной частицы направлена под углом α к вектору магнитной индукции (рис. 3.2), то модуль силы Лоренца выражается формулой FЛ = Bqυ sinα.
Обратите внимание: если скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю.
а) перпендикулярно вектору магнитной индукции?
|
|
|



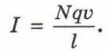

 1. Электрон движется со скоростью υ = 10 км/с вблизи поверхности Земли. Индукция магнитного поля Земли в средних широтах составляет около 5 • 10-5 Тл. Во сколько раз сила, действующая на электрон со стороны магнитнодго поля Земли, больше силы тяжести, если скорость электрона направлена:
1. Электрон движется со скоростью υ = 10 км/с вблизи поверхности Земли. Индукция магнитного поля Земли в средних широтах составляет около 5 • 10-5 Тл. Во сколько раз сила, действующая на электрон со стороны магнитнодго поля Земли, больше силы тяжести, если скорость электрона направлена: