|
|
|
|
|
§ 3. Сила Лоренца Модуль силы ЛоренцаВ предыдущем параграфе мы рассматривали силу Ампера, действующую на проводник с током, помещённый в магнитное поле. Но проводник с током отличается от проводника, в котором тока нет, только тем, что в проводнике с током есть направленное движение заряженных частиц. Следовательно,
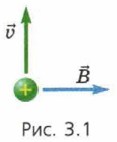
Силу, действующую на заряженную частицу, движущуюся в магнитном поле, называют силой Лоренца в честь голландского физика X. Лоренца, изучавшего движение заряженных частиц в электрическом и магнитном полях. Модуль и направление силы Лоренца можно найти, зная модуль и направление силы Ампера. Докажем, что когда скорость заряженной частицы FЛ = Bqυ, (1)
где q — заряд частицы. Как мы уже знаем, модуль силы Ампера, действующей на прямолинейный проводник с током, перпендикулярный вектору магнитной индукции, выражается формулой (см. § 2): FА = ВIl, (2) где В — модуль магнитной индукции, I — сила тока в проводнике, l — длина проводника. По определению, сила тока
где Q — заряд, который проходит через поперечное сечение проводника за время t. В качестве t удобно выбрать промежуток времени, в течение которого все свободные заряды, содержащиеся в проводнике длиной l, пройдут через поперечное сечение проводника. Если обозначить α среднюю скорость направленного движения свободных зарядов, то
|
|
|



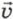 перпендикулярна вектору магнитной индукции
перпендикулярна вектору магнитной индукции 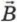 (рис. 3.1), модуль силы Лоренца выражается формулой
(рис. 3.1), модуль силы Лоренца выражается формулой