§ 4. Проводники и заряженные частицы в магнитном поле: Дополнительные вопросы и задания

13. Металлический стержень длиной l и массой m подвешен на двух проводящих нитях длиной L каждая (рис. 4.1). Система находится в однородном магнитном поле с индукцией В. Вектор магнитной индукции направлен вертикально вниз. По стержню пропустили кратковременный ток, после чего он стал совершать колебания. За время протекания тока по стержню прошёл заряд q, углом отклонения нитей от вертикали за это время можно пренебречь.

а) На какую максимальную высоту от положения равновесия поднимается стержень при колебаниях?
б) Чему равна сила натяжения каждой нити при максимальном отклонении стержня во время колебаний?

Подсказка. При максимальном отклонении центростремительное ускорение стержня равно нулю. Поэтому проекция равнодействующей приложенных к стержню сил на направление нитей равна нулю. Учтите, что нитей две.

14. Металлический стержень длиной l и массой m лежит на гладком столе и соединён одинаковыми лёгкими проводящими пружинами жёсткостью k каждая с укреплённой на столе планкой (рис. 4.9). Система находится в однородном магнитном поле. Вектор магнитной индукции направлен вертикально, модуль магнитной индукции равен В. После того как по стержню пропустили кратковременный ток, он стал совершать гармонические колебания. За время протекания тока по стержню прошел заряд Q, смещением стержня за это время можно пренебречь.

Рис. 4.9

а) Чему равна кинетическая энергия стержня сразу после выключения тока?
б) Чему равна амплитуда колебаний стержня?

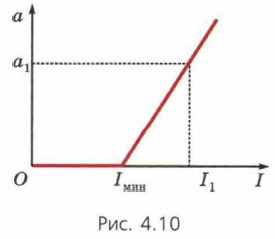
Подсказка. Воспользуйтесь законом сохранения энергии и выражением для потенциальной энергии упругой деформации. Учтите, что пружин две.

15. На горизонтальных рельсах, находящихся в вертикальном магнитом поле, лежит металлический стержень (см. рис. 4.2). Расстояние между рельсами равно l, модуль магнитной индукции равен В. На рисунке 4.10 изображён график зависимости ускорения стержня от силы тока в нём (значения I_мин, I₁, а₁ заданы). В начальный момент стержень покоится.

Рис. 4.10

а) Чему равна масса m стержня?
б) Чему равен коэффициент трения μ между стержнем и рельсами?

Подсказка. Выразите ускорение стержня через данные в условии величины, силу тока I в стержне, массу стержня m и коэффициент трения μ между стержнем и рельсами. Сопоставьте полученную формулу для линейной функции с приведённым графиком.

Окончание >>>