|
|
|
|
|
§ 13. Более сложные вопросы колебаний Фаза колебанийВернемся к уравнению х" = -ω2x, (1) решением которого, как мы уже знаем, является x = xmax cos ωt. (2) Но это — не единственное решение уравнения (1)! У него бесконечно много решений, потому что его решением является функция х = Acos(ωt + φ0) (3) с произвольными постоянными А и φ0.
Каков же смысл входящих в формулу (3) постоянных А и φ0? Нетрудно догадаться, что А равна по модулю амплитуде колебаний хmax. А чтобы понять смысл постоянной φ0, рассмотрим выражение, стоящее в формуле (3) под знаком косинуса. Его называют фазой колебаний и обозначают обычно буквой φ: φ = ωt + φ0. (4) Измеряют фазу колебаний в радианах. Обычно рассматривают изменение фазы в течение одного периода колебаний.
Постоянную φ0 в выражении для фазы колебаний, то есть значение фазы колебаний при t = 0, называют начальной фазой. Будем считать, что если уравнение колебаний выражается формулой х = хmax cos ωt, начальная фаза равна нулю.
х = хmax sin ωt, то начальная фаза колебаний равна Подсказка. Воспользуйтесь тем, что Если два колебания происходят с одной частотой, но отличаются начальными фазами, то говорят, что между ними есть сдвиг фаз. В частности, если сдвиг фаз между двумя колебаниями равен π, то говорят, что эти колебания находятся в противофазе.
|
|
|



 1. Проверьте, что функция (3) удовлетворяет уравнению (1).
1. Проверьте, что функция (3) удовлетворяет уравнению (1).
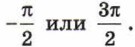
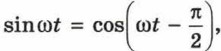 а также периодичностью тригонометрических функций.
а также периодичностью тригонометрических функций.