|
|
|
|
|
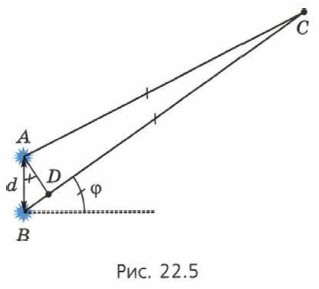
§ 22. Интерференция волн Интерференция волн на поверхности воды (окончание)Чтобы понять происхождение линий максимумов и минимумов, рассмотрим результат сложения волн в точке С, удалённой от точечных источников волн А и B на расстояние, намного превышающее расстояние d между источниками (рис. 22.5).
Обозначим φ угол между направлением на точку С (практически одинаковым для обоих источников) и перпендикуляром к линии АВ. Возьмём на ВС точку В, для которой DC = АС. Для волн, пришедших из точек А и В в точку С, разность хода волн Δd = BD. Поскольку точка С находится от точек А и В на расстоянии, большом по сравнению с d, угол при вершине С равнобедренного треугольника ACD очень мал. Следовательно, углы CAD и CDA при основании этого треугольника очень близки к прямым углам4. Поэтому треугольник ADB с хорошей точностью можно считать прямоугольным с прямым углом D. 4 Напомним, что сумма углов треугольника равна 180°.
Δd = dsin φ. (3) Подсказка. Воспользуйтесь рисунком 22.5. Вспомним теперь формулы (1) и (2), выражающие условия интерференционных максимумов и минимумов. Из этих формул и формулы (3) следует, что интерференционные максимумы будут наблюдаться под углами φk, удовлетворяющими уравнению dsin φk = kλ, (4) где k — целое число. Каждому из этих уравнений (с любым целым k) соответствует прямая. Это и есть те прямые, вдоль которых расположены интерференционные максимумы на рисунке 22.2. Интерференционный максимум, соответствующий нулевой разности хода волн (k = 0), расположен на горизонтальной прямой. Его называют центральным максимумом (максимумом нулевого порядка). На рисунке 22.2 он отмечен голубой линией. Следующий максимум, соответствующий k = 1, называют первым интерференционным максимумом (первого порядка); соответствующий k = 2 — вторым (второго порядка) и т. д.
|
|
|



 4. Объясните, почему
4. Объясните, почему