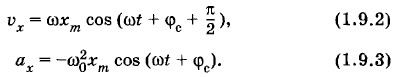|
|
|
|
|
Глава 1. Механические колебания § 1.9. Вынужденные колебания
Наиболее простой способ возбуждения незатухающих колебаний состоит в том, что на систему действует внешняя периодическая сила. Колебания под действием внешней периодической силы называются вынужденными. Работа этой силы над системой обеспечивает приток энергии к системе извне, который и не дает колебаниям затухать, несмотря на действие сил трения. Под влиянием периодической силы любое тело или система совершает колебания. Но если система сама по себе не способна совершать колебания, то ничего интересного в ней под действием периодической силы не произойдет. Вспомните пример с книгой, которую можно двигать рукой по столу слева направо и справа налево. Если же система способна совершать свободные колебания, то действие на нее периодической внешней силы вызывает весьма интересные и практически важные явления. С ними знакомы все, кому приходилось раскачивать ребенка на качелях. Качели — это маятник, обладающий определенной собственной частотой. Значительно отклонить качели от положения равновесия трудно. Постоянная во времени сила здесь мало эффективна. Не раскачает качели взрослый человек и в том случае, если он будет их беспорядочно подталкивать в разные стороны. Однако, если начать работать в правильном ритме, подталкивая качели вперед каждый раз, когда они поравняются с нами, можно без больших усилий раскачать их очень сильно. Правда, для этого потребуется некоторое время*. * Человек на качелях может самостоятельно раскачаться. Для этого он должен приседать при наибольших отклонениях качелей от положения равновесия и выпрямляться в положении равновесия. Такие колебания, называемые параметрическими, мы рассматривать не будем. Раскачать качели до больших амплитуд можно только под действием такой периодической внешней силы, которая изменяется с частотой, равной частоте свободных колебаний качелей (маятника). Вот эта возможность резкого увеличения амплитуды колебаний маятника или любой другой системы, способной совершать свободные колебания, при совпадении частоты внешней силы с собственной частотой колебательной системы и представляет главный интерес. Наблюдение вынужденных колебаний
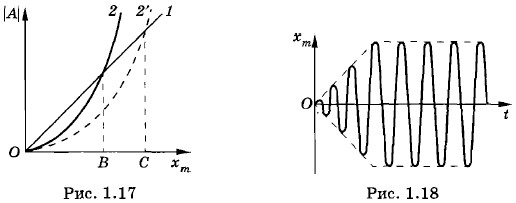
Давайте подробнее познакомимся с вынужденными колебаниями системы, обладающей собственной частотой колебаний. Рассмотрим вместо маятника груз, подвешенный на пружине. Но теперь верхний конец пружины будет прикреплен к «колену» изогнутой оси (рис. 1.16). Если вращать ось с помощью рукоятки, то на груз, прикрепленный к пружине, начнет действовать периодическая внешняя сила. Еще лучше вращать ось с помощью электродвигателя. Это обеспечит большую стабильность частоты внешней силы. Постепенно груз начнет раскачиваться. Амплитуда его колебаний нарастает. Спустя некоторое время колебания приобретут установившийся характер: их амплитуда со временем перестанет изменяться. Присмотревшись внимательно, вы обнаружите, что частота колебаний груза будет в точности равна частоте колебаний точки подвеса пружины, т. е. частоте изменения внешней силы. (Эта частота равна угловой скорости вращения рукоятки.) В этом ничего неожиданного нет. Если толкать груз вверх и вниз, то он в конце концов начнет качаться с той же частотой, с которой вы действуете на него. Установление колебанийНо почему с течением времени устанавливается определенная амплитуда колебаний? Проще всего это можно понять, исходя из энергетических соображений. Внешняя сила совершает за период работу А1, которая, конечно, прямо пропорциональна амплитуде колебаний (рис. 1.17, график 1). Ведь работа всегда пропорциональна пройденному пути. За счет этой работы увеличивается энергия колеблющегося тела и, следовательно, размах колебаний. Одновременно с ростом амплитуды колебаний растут потери механической энергии в системе. Силы трения за период совершают работу А2. При этом от системы отбирается механическая энергия. Работа сил сопротивления также пропорциональна амплитуде, так как с увеличением амплитуды растет пройденный телом путь. Но нужно еще учесть, что сама сила сопротивления, если считать ее прямо пропорциональной скорости Ведь чем больше амплитуда колебаний, тем быстрее при заданном периоде движется колеблющееся тело. В результате работа А2 оказывается пропорциональной квадрату амплитуды (рис. 1.17, график 2). При раскачке колебаний, когда амплитуда еще мала, |А2| < |A1|. Энергия системы увеличивается, и амплитуда колебаний растет. Но работа сил сопротивления увеличивается (по модулю) быстрее, чем работа внешних сил: она ведь пропорциональна не первой степени, а квадрату амплитуды. Поэтому наступит момент, когда работа сил сопротивления сравняется по модулю с работой внешних сил. Тогда механическая энергия системы перестанет нарастать и колебания установятся. В дальнейшем они будут совершаться с постоянной амплитудой (рис. 1.18), а частота колебаний будет равна частоте изменения внешней силы.
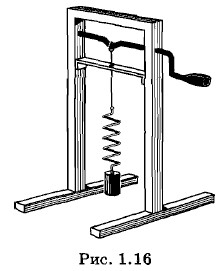
Чем меньшее сопротивление испытывает система, тем большую амплитуду будут иметь установившиеся колебания. Работа сил сопротивления пропорциональна коэффициенту сопротивления k1, и равенство |А'2| = |А1| (соответствующее пересечению графиков 1 и 2', см. рис. 1.17) при малом сопротивлении (k'1 < k1), может быть достигнуто при большей амплитуде (ОС > ОB). Разумеется, при этом требуется и большее время для того, чтобы колебания установились. Установившиеся вынужденные колебания происходят с частотой со и амплитудой хm по гармоническому закону: х = хm cos (ωt + φс). (1.9.1) Внешне вынужденные установившиеся колебания выглядят так же, как и свободные колебания в системе без трения. Но если при свободных колебаниях амплитуда хm и начальная фаза φ0 определяются начальными условиями, то при вынужденных колебаниях хm и φс определяются (как мы увидим в дальнейшем) параметрами самой системы и внешней силой. Прежде всего играет существенную роль соотношение частот собственных и вынужденных колебаний. Величина φс в случае вынужденных колебаний — это не начальная фаза, а сдвиг фаз между колебаниями координаты и внешней силы. Скорость и ускорение при вынужденных колебаниях определяются такими же уравнениями, как и при свободных колебаниях:
|
|
|



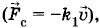 растет пропорционально амплитуде.
растет пропорционально амплитуде.