|
|
|
|
|
Глава 1. Механические колебания Вынужденные колебанияУравнение движения для вынужденных колебанийПриступим к решению основной задачи: выясним, от чего и как зависят амплитуда хm вынужденных колебаний и сдвиг фаз φс. Для этого запишем и исследуем уравнение движения для вынужденных колебаний. Пусть на колебательную систему (груз на пружине) действует внешняя периодическая сила Fx = Fm cos ωt. Кроме того, на тело действует сила упругости (Fу)x = -kx и сила сопротивления, пропорциональная скорости: (Fc)x = -k1υx, где k1 — коэффициент сопротивления. (При малых скоростях движения тела силу сопротивления можно считать пропорциональной скорости.) Тогда уравнение движения запишется так:
Перенеся в левую часть уравнения все силы, кроме внешней, получим:
Удобнее записать это уравнение в несколько другом виде, разделив правую и левую его части на m и введя собственную частоту
Движение тела, подчиняющееся этому уравнению, достаточно сложно, особенно вначале, когда оно не является гармоническим. Мы рассмотрим лишь три предельных случая. Первый случай: Второй случай: ω >> ω0; выполняется противоположное условие. И наконец, самый важный случай: * Необходимо сделать одно уточнение. При наличии сил сопротивления собственная частота ωc свободных колебаний не равна Вынужденные колебания малой частотыЕсли ω << ω0, то из трех членов левой части уравнения (1.9.5) самым большим будет последний член Отсюда
Колебания координаты происходят с амплитудой
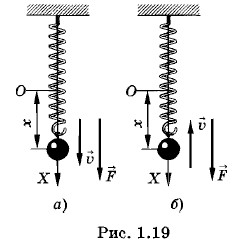
С энергетической точки зрения условия для перекачки энергии в колебательную систему от внешних тел, действующих на систему с периодической силой, в данном случае очень неблагоприятны. В самом деле: четверть периода, когда тело смещается от положения равновесия, внешняя сила совершает положительную работу, так как сила и скорость тела, а значит, и перемещение направлены в одну сторону (рис. 1.19, a). Но в следующую четверть периода, когда тело возвращается к положению равновесия, сила и скорость (а значит, и перемещение) направлены в противоположные стороны (рис. 1.19, б). Работа внешней силы при этом отрицательна. Та же картина будет наблюдаться во вторую половину периода. В целом за период работа внешней силы почти точно равна нулю. Лишь малая часть работы внешней силы идет на компенсацию работы силы трения, так как скорость движения тела при ω << ω0 очень мала, и поэтому мало значение силы трения. Здесь имеется некоторая тонкость, иногда затрудняющая понимание сути дела. Если смещение от положения равновесия прямо пропорционально силе в любой момент времени, то казалось бы на первый взгляд, что работа должна быть все время положительной. Однако надо иметь в виду, что знак работы зависит от совпадения направления силы и направления перемещения, т. е. скорости, а не знака координаты. Для того чтобы работа была положительной, необходимо совпадение знаков Fх и Δx: Надо хорошо представлять себе, что когда сила и координата достигают максимальных значений, то после этого сила начинает уменьшаться, не меняя направления, а скорость меняет направление. Вынужденные колебания большой частотыВ случае ω >> ω0 в левой части уравнения (1.9.5) наибольшим будет первый член, амплитуда которого пропорциональна квадрату частоты. Он играет основную роль и поэтому можно записать
По фазе с колебаниями силы совпадают теперь не колебания координаты, а колебания ускорения. Колебания координаты происходят в противофазе с колебаниями внешней силы. Амплитуда координаты равна:
Таким образом, колебания тела происходят по закону
При ω → ∞ (это эквивалентно условию ω >> ω0) хm → 0, т. е. амплитуда колебаний мала. Этот результат вполне естествен. Сила столь быстро меняет направление, что тело, обладающее инертностью, не успевает заметно сдвинуться относительно положения равновесия. Половину периода внешняя сила совершает положительную работу, а другую половину — отрицательную. Половину периода сила и перемещение направлены одинаково, а другую половину периода они направлены в противоположные стороны. Энергия опять почти не поступает в систему.
|
|
|



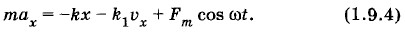
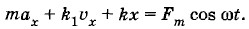
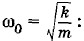
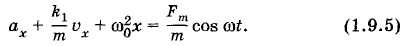
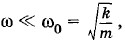 т. е. частота внешней периодической силы много меньше частоты собственных колебаний системы.
т. е. частота внешней периодической силы много меньше частоты собственных колебаний системы.
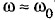 .* Это случай резонанса.
.* Это случай резонанса.
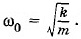 На самом деле она несколько меньше:
На самом деле она несколько меньше: 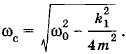 Но при малом коэффициенте сопротивления (k → 0) ωc ≈ ω0. Практически наиболее интересен именно такой случай. Поэтому мы с полным основанием можем считать собственную частоту колебаний системы равной ω0.
Но при малом коэффициенте сопротивления (k → 0) ωc ≈ ω0. Практически наиболее интересен именно такой случай. Поэтому мы с полным основанием можем считать собственную частоту колебаний системы равной ω0.
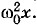 Действительно, амплитуда первого слагаемого пропорциональна ω2xm, второго — ωxm последнего —
Действительно, амплитуда первого слагаемого пропорциональна ω2xm, второго — ωxm последнего — 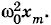 Поэтому приближенно (учитывая, что ω → 0) имеем:
Поэтому приближенно (учитывая, что ω → 0) имеем:
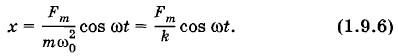
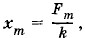 а фаза колебаний совпадает с фазой колебаний внешней силы. Отметим, что амплитуда колебаний тем меньше, чем больше жесткость пружины. Качественно этот случай можно описать так. При малой частоте изменения внешней силы происходит почти то же самое, что и при действии на пружину постоянной силы. В соответствии с законом Гука смещение увеличивается пропорционально внешней силе, и в любой момент внешняя сила почти точно уравновешивается силой упругости пружины.
а фаза колебаний совпадает с фазой колебаний внешней силы. Отметим, что амплитуда колебаний тем меньше, чем больше жесткость пружины. Качественно этот случай можно описать так. При малой частоте изменения внешней силы происходит почти то же самое, что и при действии на пружину постоянной силы. В соответствии с законом Гука смещение увеличивается пропорционально внешней силе, и в любой момент внешняя сила почти точно уравновешивается силой упругости пружины.
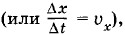 а не Fх и x.
а не Fх и x.


