|
|
|
|
|
Глава 1. Механические колебания
§ 1.10. Резонанс
В этом случае первый член уравнения (1.9.5), который можно записать так:
взаимно уничтожается с третьим членом, равным В результате уравнение (1.9.5) принимает вид
Это простое уравнение отражает всю суть явления. При ω ≈ ω0 в любой момент времени (еще раз подчеркнем, что речь идет об установившихся колебаниях) внешняя сила как бы исключает из игры силу сопротивления. В результате ускорение телу сообщается только силой упругости пружины. В сущности, реализуется очень необычная ситуация: гармонические колебания существуют в системе сколь угодно длительное время, несмотря на действие силы сопротивления. Из уравнения (1.10.1) видно, что при ω ≈ ω0 фаза колебаний скорости совпадает с фазой колебаний внешней силы. Работа внешней силы при этих условиях положительна на всем протяжении периода. Создаются оптимальные условия для перекачки энергии от внешних тел к колебательной системе. Положительная работа внешней силы в точности равна по модулю отрицательной работе силы сопротивления. Из-за этого механическая энергия за счет работы силы сопротивления переходит во внутреннюю энергию (пружина с грузом и окружающий воздух нагреваются). Амплитуда колебаний при ω ≈ ω0 равна:
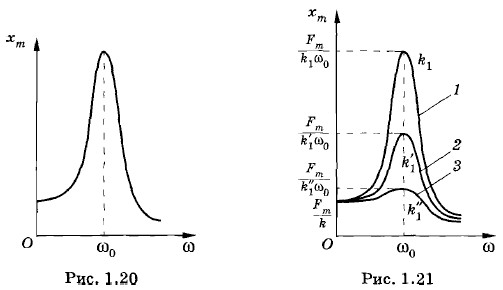
При k1 → 0 хm → ∞, т. е. очевидно, что при ω ≈ ω0 амплитуда максимальна. Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний называется резонансом*. *От латинского слова resonans — дающий отзвук. Наблюдать явление резонанса можно с помощью установки, изображенной на рисунке 1.16. Плавно увеличивая частоту внешней силы, мы заметим, что амплитуда колебаний растет. Она достигает максимума, когда внешняя сила действует в такт со свободными колебаниями (ω ≈ ω0). При дальнейшем увеличении частоты амплитуда установившихся колебаний опять уменьшается (рис. 1.20). Влияние сопротивления на резонансСущественное влияние на резонанс оказывает сопротивление в системе. Если коэффициент сопротивления k1 имеет достаточно большое значение, то согласно уравнению (1.10.2) резонансная амплитуда колебаний невелика. При резонансе положительная работа внешней силы целиком идет на покрытие расхода энергии за счет отрицательной работы силы сопротивления. Чем меньше сила сопротивления, тем больше амплитуда установившихся колебаний. Изменение амплитуды колебаний в зависимости от частоты при различных коэффициентах сопротивления и одной и той же амплитуде внешней силы графически изображено на рисунке 1.21. Кривой 1 соответствует минимальный коэффициент сопротивления, а кривой 3 — максимальный. На этом рисунке хорошо видно, что возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше сопротивление в системе. При малом коэффициенте сопротивления резонанс «острый» , а при большом «тупой». Если частота колебаний далека от резонансной, то амплитуда колебаний мала и почти не зависит от силы сопротивления в системе. В системе с малым сопротивлением амплитуда колебаний при резонансе может быть очень большой даже в том случае, когда внешняя сила мала. Но надо хорошо уяснить, что большая амплитуда установится только спустя продолжительное время после начала действия внешней силы. В соответствии с законом сохранения энергии заставить систему колебаться с большой амплитудой, а значит, сообщить ей большую энергию с помощью сравнительно небольшой внешней силы, можно только за большой промежуток времени. Если сопротивление велико, то амплитуда колебаний будет небольшой и для установления колебаний не потребуется много времени. О резонансе имеет смысл говорить, если затухание свободных колебаний в системе мало. Иначе амплитуда вынужденных колебаний при ω ≈ ω0 мало отличается от амплитуды колебаний при других частотах. В этом можно убедиться, помещая колеблющийся груз в вязкую жидкость.
|
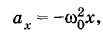
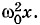Эти два члена в любой момент времени одинаковы по модулю, но имеют противоположные знаки, так как ускорение и координата при любом гармоническом колебании сдвинуты по фазе на π.
|
|