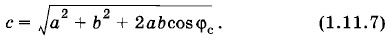|
|
|
|
|
Глава 1. Механические колебания § 1.11. Сложение гармонических колебаний. Спектр колебаний
* Имеет смысл отметить, что такая простая картина возникает только в линейных колебательных системах, в которых сила, возвращающая тело в положение равновесия, прямо пропорциональна смещению от положения равновесия. Если же возвращающая сила зависит от смещения нелинейно, то картина колебаний чрезвычайно сильно усложняется. Результирующее колебание уже не является простой суммой отдельных колебаний. Такие сложные нелинейные системы мы рассматривать не будем. Правда, именно изучение колебаний в нелинейных системах представляет наибольший теоретический и практический интерес в современной физике.
Наиболее просто складываются гармонические колебания одинаковых частот. Предварительно рассмотрим проекцию вращающегося вектора. Пусть вектор Модуль вектора φ = ωt + φ0. (1.11.1) Проекция вектора х = a cos φ = a cos (ωt + φ0). (1.11.2) Одновременно- проекция этого вектора на ось Y оказывается равной у = a sin (ωt + φ0). (1.11.3) Мы получили простой, но важный результат.
Сложение гармонических колебаний одинаковых частотСложение колебаний одинаковых частот проще всего осуществить c помощью так называемой векторной диаграммы.
Построение векторной диаграммы основано на известном факте: проекция результирующего вектора равна сумме проекций слагаемых векторов. Поэтому сложение гармонических колебаний x1 = a cos (ωt + φ01) и х2 = b cos (ωt + φ02) (1.11.4)
осуществляется так. Строят векторы φc = φ02- φ01, (1.11.5) представляет собой сдвиг фаз между этими колебаниями. Так как частоты складываемых колебаний равны, то угол φc между векторами Проекция суммарного вектора x = х1 + х2 = c cos (ωt + φ0). (1.11.6) Оно происходит с той же частотой ю, что и колебания х1 и х2. Модуль с вектора
Амплитуда результирующего колебания зависит от амплитуд складываемых колебаний а и b и сдвига фаз между ними. С помощью рисунка 1.25 можно найти и начальную фазу φ0.
|
|
|



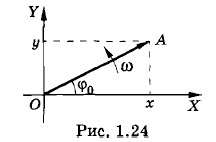
 вращается с постоянной угловой скоростью ω вокруг оси, проходящей через точку О (рис. 1.24).
вращается с постоянной угловой скоростью ω вокруг оси, проходящей через точку О (рис. 1.24).
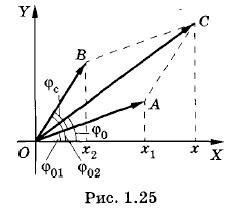
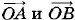 , изображающие первое и второе колебания (рис. 1.25). Их модули равны амплитудам складываемых колебаний, а угол между ними, равный
, изображающие первое и второе колебания (рис. 1.25). Их модули равны амплитудам складываемых колебаний, а угол между ними, равный
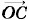 представляет собой результирующее колебание:
представляет собой результирующее колебание: